题目内容
4.记函数f(x)的导数为f(1)(x),f(1)(x)的导数为f(2)(x),…,f(n-1)(x)的导数为f(n)(x)(n∈N*),若f(x)可进行n次求导,则f(x)均可近似表示为:f(x)≈f(0)+$\frac{{{f^{(1)}}(0)}}{1!}x+\frac{{{f^{(2)}}(0)}}{2!}{x^2}+\frac{{{f^{(3)}}(0)}}{3!}{x^3}$+…+$\frac{{{f^{(n)}}(0)}}{n!}{x^n}$,若取n=4,根据这个结论,则可近似估计cos2≈-$\frac{1}{3}$(用分数表示).分析 f(x)=cosx,f(1)(x)=-sinx,f(2)(x)=-cosx,f(3)(x)=sinx,f(4)(x)=cosx,…,可得T=4,代入即可得出.
解答 解:f(x)=cosx,f(1)(x)=-sinx,f(2)(x)=-cosx,f(3)(x)=sinx,f(4)(x)=cosx,…,∴T=4,
∴当n=4时,f(2)=cos2=f(0)+0×2+$\frac{-1}{2!}×{2}^{2}$+$\frac{0}{3!}×{2}^{4}$=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查了导数的运算法则、三角函数的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
14.下列四个方程中表示y是x的函数的是( )
①x=y2②y=1-x2③y=$\frac{1}{2}$x-3④y2=1-x.
①x=y2②y=1-x2③y=$\frac{1}{2}$x-3④y2=1-x.
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②④ |
15.已知全集U={1,2,3,4,5,6},A={2,4,5},B={1,3,5},则(∁UA)∩(∁UB)=( )
| A. | [6} | B. | {5} | C. | {1,2,3,4} | D. | {5,6} |
16.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-x2+1 | C. | y=-e-x-ex | D. | y=sinx |
13.设集合M={x|1<x<5},N={0,2,3,5},则M∩N=( )
| A. | {x|2<x<4} | B. | {0,2,3} | C. | {2,3} | D. | {x|2<x<3} |
 如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求:
如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求: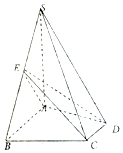 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.