题目内容
已知定点A（-1，
），动点P按逆时针方向沿着单位圆从P0（1，0）处开始运动（t=0秒），且每秒运动的弧长为
弧度，在t秒内（t＞0）到达点P．记函数f（t）=
•
，向量
=
+
，关于f（t）有以下结论：
①f（t）=-
sin
t+cos
t；②f（t）=2sin（
t-
）；③Q点的轨迹是以A为圆心，半径为1的圆；
④当f（t）第一次取得最大值时，需要的时间是t=
秒；⑤1≤|
|≤3
其中正确的是 ．
| 3 |
| π |
| 5 |
| OA |
| OP |
| OQ |
| OA |
| OP |
①f（t）=-
| 3 |
| π |
| 5 |
| π |
| 5 |
| π |
| 5 |
| π |
| 6 |
④当f（t）第一次取得最大值时，需要的时间是t=
| 3 |
| 10 |
| OQ |
其中正确的是
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据数量积之间的关系求出函数f（t）的表达式，然后根据三角函数的图象和性质分别进行判断即可．
解答：
解：动点P按逆时针方向沿着单位圆从P0（1，0）处开始运动（t=0秒），且每秒运动的弧长为
弧度，
∴P点的坐标为（cos
t，sin
t），
=（-1，
），
=（cos
t，sin
t），
∴f（t）=
•
=-cos
t+
sin
t=2sin（
t-
），
∴①错误，②正确，
∵
=
+
=（-1+cos
t，
+sin
t）
∴设Q（x，y），
则x=-1+cos
t，y=
+sin
t，消去参数得（x+1）2+（y-
）2=1，
∴Q点的轨迹是以A为圆心，半径为1的圆，
∴③正确．
由
t-
=
，解得t=
，∴④错误．
∵
2=（-1+cos
t）2+（
+sin
t）2=5+4sin（
t-
），
∴1≤5+4sin（
t-
）≤9，
∴1≤
2≤9，
即1≤|
|≤3，∴⑤正确．
故答案为：②③⑤
| π |
| 5 |
∴P点的坐标为（cos
| π |
| 5 |
| π |
| 5 |
| OA |
| 3 |
| OP |
| π |
| 5 |
| π |
| 5 |
∴f（t）=
| OA |
| OP |
| π |
| 5 |
| 3 |
| π |
| 5 |
| π |
| 5 |
| π |
| 6 |
∴①错误，②正确，
∵
| OQ |
| OA |
| OP |
| π |
| 5 |
| 3 |
| π |
| 5 |
∴设Q（x，y），
则x=-1+cos
| π |
| 5 |
| 3 |
| π |
| 5 |
| 3 |
∴Q点的轨迹是以A为圆心，半径为1的圆，
∴③正确．
由
| π |
| 5 |
| π |
| 6 |
| π |
| 2 |
| 10 |
| 3 |
∵
| OQ |
| π |
| 5 |
| 3 |
| π |
| 5 |
| π |
| 5 |
| π |
| 6 |
∴1≤5+4sin（
| π |
| 5 |
| π |
| 6 |
∴1≤
| OQ |
即1≤|
| OQ |
故答案为：②③⑤
点评：本题主要考查三角函数的图象和性质，利用向量数量积之间的关系求出函数的表达式是解决本题的关键，综合性较强，运算量较大．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
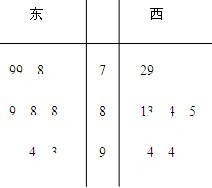某城市要建成宜商、宜居的国际化新城，该城市的东城区、西城区分别引进8个厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示．设y=x4+ln3，则y′=（ ）
| A、4x3 | ||
B、4x3+
| ||
| C、x4lnx | ||
D、x4lnx+
|