题目内容
已知函数f (x)=lnx.
(Ⅰ)函数g(x)=3x-2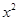 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
(Ⅱ)函数h(x)=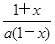 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
G(x)<-2,求实数a的取值范围.
(Ⅰ)函数g(x)=3x-2
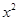 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;(Ⅱ)函数h(x)=
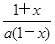 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),G(x)<-2,求实数a的取值范围.
(Ⅰ)函数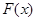 的单调递增区间为
的单调递增区间为 ;函数
;函数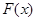 的单调递减区间为
的单调递减区间为 .(Ⅱ)实数
.(Ⅱ)实数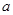 的取值范围是
的取值范围是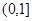 .
.
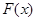 的单调递增区间为
的单调递增区间为 ;函数
;函数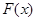 的单调递减区间为
的单调递减区间为 .(Ⅱ)实数
.(Ⅱ)实数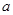 的取值范围是
的取值范围是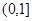 .
.(1)求出F(x),利用导数大(小)于零,确定其单调增(减)区间即可.
(2)先求出G(x)的表示式,然后本题可转化为以任意x∈(0,1), G(x)max<-2,然后求G(x)的最大值即可.
(Ⅰ)函数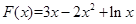 ,其定义域为
,其定义域为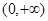 .…………………………1分
.…………………………1分

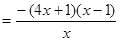
 .……………3分
.……………3分
当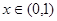 ,
, ,函数
,函数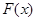 单调递增,……………………4分
单调递增,……………………4分
当 ,
,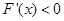 ,函数
,函数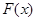 单调递减,………………………………5分
单调递减,………………………………5分
∴函数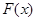 的单调递增区间为
的单调递增区间为 ;函数
;函数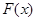 的单调递减区间为
的单调递减区间为 .……6分
.……6分
(Ⅱ)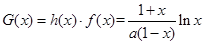 ,由已知
,由已知 ,因为
,因为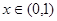 ,
,
所以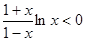 .
.
①当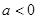 时,
时,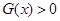 .不合题意.……………………8分
.不合题意.……………………8分
②当 时,
时,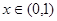 ,由
,由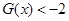 ,可得
,可得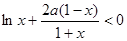 .
.
设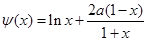 ,则
,则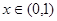 ,
,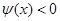 .
.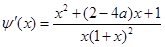 .
.
设 ,方程
,方程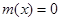 的判别式
的判别式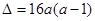 .
.
若 ,
,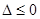 ,
,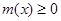 ,
,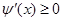 ,
,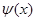 在
在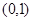 上是增函数,
上是增函数,
又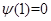 ,所以
,所以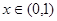 ,
,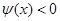 .………………………10分
.………………………10分
若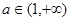 ,
,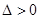 ,
, ,
, ,所以存在
,所以存在 ,使得
,使得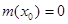 ,对任意
,对任意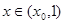 ,
, ,
,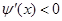 ,
,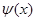 在
在 上是减函数,
上是减函数,
又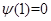 ,所以
,所以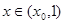 ,
, .不合题意综上,实数
.不合题意综上,实数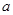 的取值范围是
的取值范围是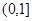
(2)先求出G(x)的表示式,然后本题可转化为以任意x∈(0,1), G(x)max<-2,然后求G(x)的最大值即可.
(Ⅰ)函数
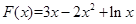 ,其定义域为
,其定义域为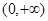 .…………………………1分
.…………………………1分
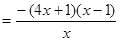
 .……………3分
.……………3分当
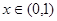 ,
, ,函数
,函数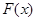 单调递增,……………………4分
单调递增,……………………4分当
 ,
,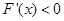 ,函数
,函数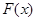 单调递减,………………………………5分
单调递减,………………………………5分∴函数
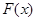 的单调递增区间为
的单调递增区间为 ;函数
;函数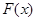 的单调递减区间为
的单调递减区间为 .……6分
.……6分(Ⅱ)
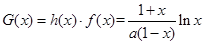 ,由已知
,由已知 ,因为
,因为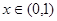 ,
,所以
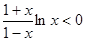 .
.①当
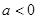 时,
时,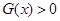 .不合题意.……………………8分
.不合题意.……………………8分②当
 时,
时,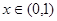 ,由
,由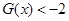 ,可得
,可得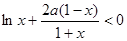 .
.设
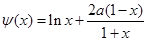 ,则
,则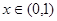 ,
,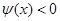 .
.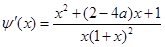 .
.设
 ,方程
,方程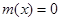 的判别式
的判别式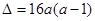 .
.若
 ,
,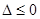 ,
,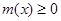 ,
,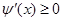 ,
,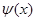 在
在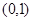 上是增函数,
上是增函数,又
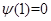 ,所以
,所以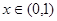 ,
,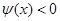 .………………………10分
.………………………10分若
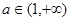 ,
,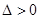 ,
, ,
, ,所以存在
,所以存在 ,使得
,使得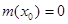 ,对任意
,对任意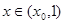 ,
, ,
,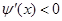 ,
,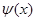 在
在 上是减函数,
上是减函数,又
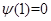 ,所以
,所以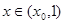 ,
, .不合题意综上,实数
.不合题意综上,实数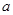 的取值范围是
的取值范围是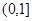

练习册系列答案
相关题目
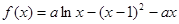 (常数
(常数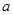
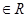 ).
).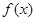 的单调区间;(5分)
的单调区间;(5分)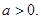 如果对于
如果对于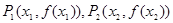
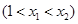 ,存在
,存在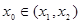 ,使得
,使得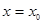 处的切线
处的切线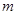 ∥
∥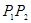 ,求证:
,求证: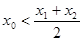 .(7分)
.(7分)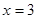 是函数
是函数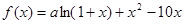 的一个极值点。
的一个极值点。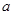 ; (2)求函数
; (2)求函数 的单调区间;
的单调区间;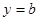 与函数
与函数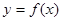 的图象有3个交点,求
的图象有3个交点,求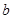 的取值范围。
的取值范围。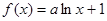
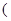
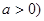 .
.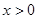 时,求证:
时,求证: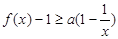 ;(4分)
;(4分)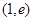 上
上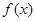
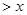 恒成立,求实数
恒成立,求实数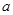 的范围。(4分)
的范围。(4分)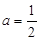 时,求证:
时,求证: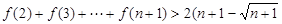 )
)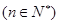 .(4分)
.(4分)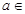 R,函数
R,函数 (x∈R).
(x∈R). 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间; 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由; 上单调递增,求
上单调递增,求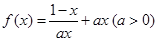 .
.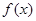 在
在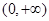 的单调性并证明;
的单调性并证明;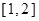 上的最小值。
上的最小值。 (a≠0)
(a≠0) ,e]的最大值;
,e]的最大值;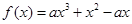 ,
,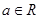 ,
,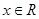 .
.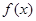 在区间
在区间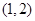 上不是单调函数,试求
上不是单调函数,试求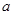 的取值范围;
的取值范围;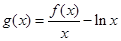
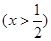 的单调递增区间;
的单调递增区间;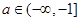 ,使函数
,使函数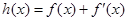 ,
,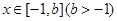 在
在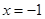 处取得最小值,试求
处取得最小值,试求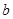 的最大值.
的最大值.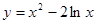 的单调增区间是( )
的单调增区间是( )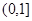 ;
;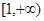 ;
; 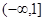 及
及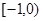 及
及