题目内容
(12分)已知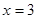 是函数
是函数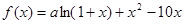 的一个极值点。
的一个极值点。
(1)求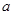 ; (2)求函数
; (2)求函数 的单调区间;
的单调区间;
(3)若直线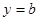 与函数
与函数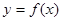 的图象有3个交点,求
的图象有3个交点,求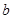 的取值范围。
的取值范围。
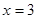 是函数
是函数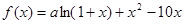 的一个极值点。
的一个极值点。(1)求
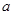 ; (2)求函数
; (2)求函数 的单调区间;
的单调区间;(3)若直线
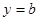 与函数
与函数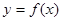 的图象有3个交点,求
的图象有3个交点,求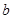 的取值范围。
的取值范围。(Ⅰ)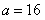 .(Ⅱ)
.(Ⅱ)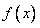 的单调增区间是
的单调增区间是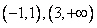 ,
,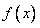 的单调减区间是
的单调减区间是 .(Ⅲ)
.(Ⅲ)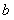 的取值范围为
的取值范围为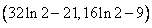 。
。
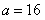 .(Ⅱ)
.(Ⅱ)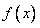 的单调增区间是
的单调增区间是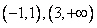 ,
,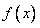 的单调减区间是
的单调减区间是 .(Ⅲ)
.(Ⅲ)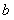 的取值范围为
的取值范围为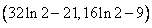 。
。本试题主要是考察了导数在研究函数的中 运用,利用函数的极值点可知导数为零得到参数的取值,然后求解析式,并利用导数来判定函数的单调性以及研究常函数与函数的交点的问题的综合运用。
(1)利用函数在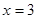 是函数
是函数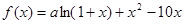 的一个极值点,说明了该点的导数值为零,得到参数的值。
的一个极值点,说明了该点的导数值为零,得到参数的值。
(2)利用第一问的结论求解导数,判定单调区间。
(3)要研究常函数与已知函数的交点问题,关键是弄清楚,函数y=f(x)与坐标轴的位置关系即可。
解:(Ⅰ)因为 ,所以
,所以 ,因此
,因此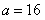 .
.
(Ⅱ)由(Ⅰ)知,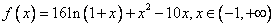 ,
,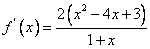 ,
,
当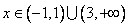 时,
时,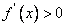 ,当
,当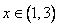 时,
时,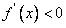 ,所以
,所以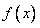 的单调增区间是
的单调增区间是
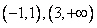 ,
,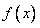 的单调减区间是
的单调减区间是 .
.
(Ⅲ)由(Ⅱ)知,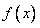 在
在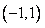 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在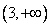 上单调增加,且当
上单调增加,且当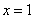 或
或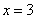 时,
时,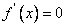 ,所以
,所以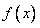 的极大值为
的极大值为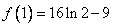 ,极小值为
,极小值为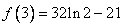 ,
,
因此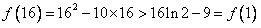 ,
,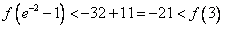 ,
,
所以在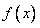 的三个单调区间
的三个单调区间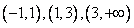 直线
直线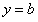 有
有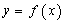 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当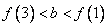 ,因此,
,因此,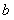 的取值范围为
的取值范围为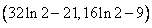 。
。
(1)利用函数在
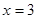 是函数
是函数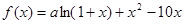 的一个极值点,说明了该点的导数值为零,得到参数的值。
的一个极值点,说明了该点的导数值为零,得到参数的值。(2)利用第一问的结论求解导数,判定单调区间。
(3)要研究常函数与已知函数的交点问题,关键是弄清楚,函数y=f(x)与坐标轴的位置关系即可。
解:(Ⅰ)因为
 ,所以
,所以 ,因此
,因此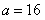 .
.(Ⅱ)由(Ⅰ)知,
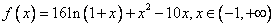 ,
,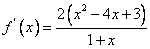 ,
,当
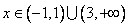 时,
时,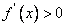 ,当
,当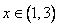 时,
时,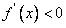 ,所以
,所以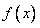 的单调增区间是
的单调增区间是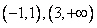 ,
,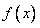 的单调减区间是
的单调减区间是 .
.(Ⅲ)由(Ⅱ)知,
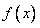 在
在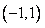 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在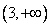 上单调增加,且当
上单调增加,且当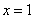 或
或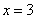 时,
时,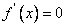 ,所以
,所以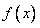 的极大值为
的极大值为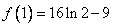 ,极小值为
,极小值为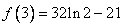 ,
,因此
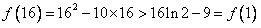 ,
,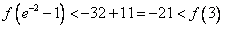 ,
,所以在
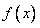 的三个单调区间
的三个单调区间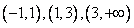 直线
直线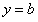 有
有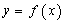 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当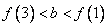 ,因此,
,因此,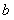 的取值范围为
的取值范围为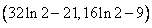 。
。
练习册系列答案
相关题目
 ,其中
,其中 。
。 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 成立。
成立。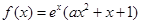 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。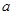 的值,并讨论
的值,并讨论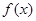 的单调性;
的单调性;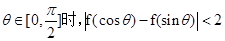
 为常数)
为常数) 上单调递增,且
上单调递增,且
 的图象在直线
的图象在直线
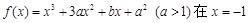 时的极值为0.
时的极值为0.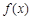 的单调区间.
的单调区间.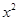 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;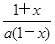 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),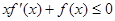 ,对任意正数a,b,若a<b,
,对任意正数a,b,若a<b,



 有极值,则导函数
有极值,则导函数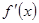 的图象不可能是 ( )
的图象不可能是 ( )
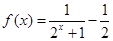 .
.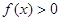 ,求实数
,求实数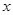 的取值范围;
的取值范围;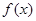 的奇偶性,并说明理由.
的奇偶性,并说明理由.