题目内容
已知函数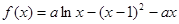 (常数
(常数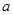
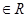 ).
).
(Ⅰ)求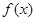 的单调区间;(5分)
的单调区间;(5分)
(Ⅱ)设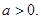 如果对于
如果对于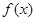 的图象上两点
的图象上两点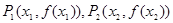
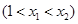 ,存在
,存在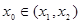 ,使得
,使得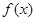 的图象在
的图象在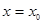 处的切线
处的切线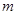 ∥
∥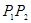 ,求证:
,求证: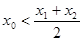 .(7分)
.(7分)
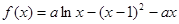 (常数
(常数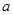
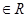 ).
).(Ⅰ)求
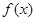 的单调区间;(5分)
的单调区间;(5分)(Ⅱ)设
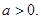 如果对于
如果对于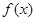 的图象上两点
的图象上两点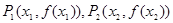
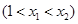 ,存在
,存在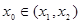 ,使得
,使得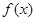 的图象在
的图象在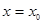 处的切线
处的切线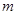 ∥
∥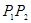 ,求证:
,求证: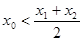 .(7分)
.(7分)(I)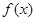 的定义域为
的定义域为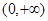
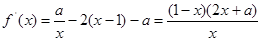 -----(1分)
-----(1分)
①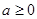 时,
时,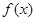 的增区间为
的增区间为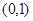 ,减区间为
,减区间为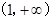
②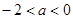 时,
时,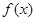 的增区间为
的增区间为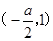 ,减区间为
,减区间为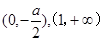
③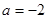 时,
时,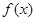 减区间为
减区间为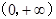
④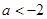 时,
时,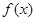 的增区间为
的增区间为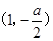 ,减区间为
,减区间为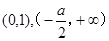
(II)见解析
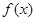 的定义域为
的定义域为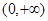
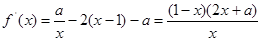 -----(1分)
-----(1分)①
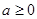 时,
时,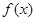 的增区间为
的增区间为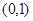 ,减区间为
,减区间为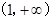
②
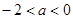 时,
时,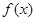 的增区间为
的增区间为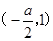 ,减区间为
,减区间为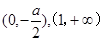
③
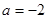 时,
时,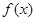 减区间为
减区间为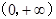
④
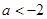 时,
时,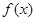 的增区间为
的增区间为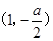 ,减区间为
,减区间为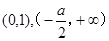
(II)见解析
(1)先确定函数f(x)的定义域,然后求导,由于含参数a,所以要对a进行讨论确定导数是大于零还是小于零,进而求得单调区间.
(2)由题意
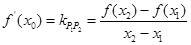
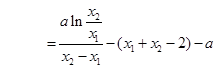
又因为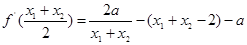 ,
,
因为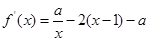 (
(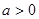 )在
)在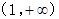 上为减函数
上为减函数
所以问题转化为要证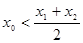 ,只要证
,只要证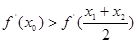
即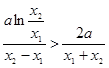 ,即证
,即证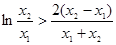 .
.
然后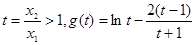 ,利用导数求g(t)的最小值即可
,利用导数求g(t)的最小值即可
(2)由题意
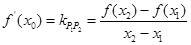
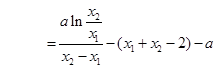
又因为
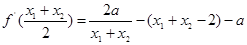 ,
,因为
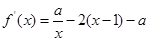 (
(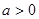 )在
)在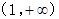 上为减函数
上为减函数所以问题转化为要证
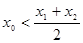 ,只要证
,只要证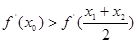
即
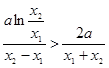 ,即证
,即证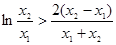 .
.然后
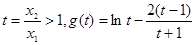 ,利用导数求g(t)的最小值即可
,利用导数求g(t)的最小值即可
练习册系列答案
相关题目
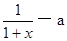 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)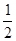
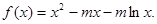
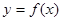 在点(1,
在点(1,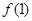 )处的切线与x轴平行.
)处的切线与x轴平行.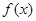 的最值;
的最值;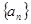 满足
满足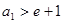 (
(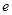 为自然对数的底数),
为自然对数的底数),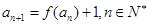 ,
,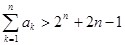 .
.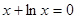 的实根为
的实根为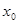 .
.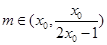 ,存在
,存在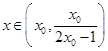 使
使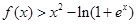 成立.
成立.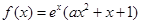 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。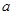 的值,并讨论
的值,并讨论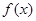 的单调性;
的单调性;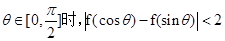
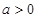 ,函数
,函数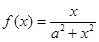 的导函数为
的导函数为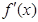 .
.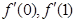 的值,并比较它们的大小;
的值,并比较它们的大小;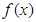 的极值.
的极值.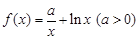 .
.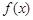 在
在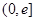 上的单调性(
上的单调性(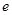 为自然对数的底);
为自然对数的底);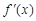 为
为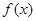 的导函数,若函数
的导函数,若函数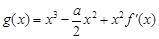 在区间
在区间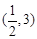 上存在极值,求实数
上存在极值,求实数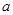 的取值范围。
的取值范围。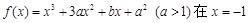 时的极值为0.
时的极值为0. 的单调区间.
的单调区间. ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;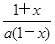 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),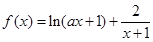 ,其中
,其中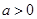 .
.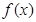 在
在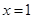 处取得极值,求曲线
处取得极值,求曲线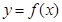 在点
在点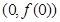 处的切线方程;
处的切线方程;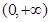 的单调性;
的单调性;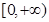 上的最小值为2,求
上的最小值为2,求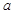 的取值范围.
的取值范围.