题目内容
9.一艘轮船在江中向正东方向航行,在点P观测到灯塔A、B在一直线上,并与航线成角α(0°<α<90°),轮船沿航线前进b米到达C处,此时观测到灯塔A在北偏西45°方向,灯塔B在北偏东β(0°<β<90°)方向,0°<α+β<90°,求CB;(结果用α,β,b表示)分析 由题意,∠B=90°-(α+β),△PBC中,运用正弦定理可得结论.
解答  解:由题意,∠B=90°-(α+β),
解:由题意,∠B=90°-(α+β),
△PBC中,PC=b,由正弦定理可得$CB=\frac{bsinα}{cos(α+β)}$.
点评 本题考查正弦定理的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
19.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=log2(x+m),则f(m-16)=( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
20.已知集合U={1,2,3,4,5,6,7},A={2,4,5,7},B={3,4,5}则(∁UA)∪B=( )
| A. | {3} | B. | {4,5} | C. | {1,3,4,5,6} | D. | {2,3,4,5,7} |
19.已知定义在$(0,\frac{π}{2})$上的函数,f′(x)为其导函数,且$\frac{f(x)}{sinx}<\frac{{{f^'}(x)}}{cosx}$恒成立,则( )
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
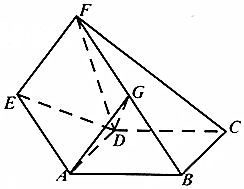 如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.
如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.