题目内容
4.梯形ABCD中,DC∥AB,DC=2,AB=4,AD=BC=3,则$\overrightarrow{AC}•\overrightarrow{BD}$=-1.分析 以A为原点,以AB所在的直线为x轴,以AB的垂线为y轴,建立如图所示的坐标系,再根据向量的数量积公式计算即可.
解答 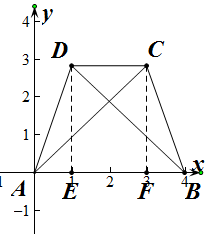 解:∵梯形ABCD中,DC∥AB,DC=2,AB=4,AD=BC=3,
解:∵梯形ABCD中,DC∥AB,DC=2,AB=4,AD=BC=3,
过点D,C作DE⊥AE,CF⊥AB,垂足分别为为E,F,
∴AE=BF=1,
∴DE=CF=$\sqrt{{3}^{2}-1}$=2$\sqrt{2}$,
以A为原点,以AB所在的直线为x轴,以AB的垂线为y轴,建立如图所示的坐标系,
∴A(0,0),B(4,0),C(3,2$\sqrt{2}$),D(1,2$\sqrt{2}$),
∴$\overrightarrow{AC}$=(3,2$\sqrt{2}$),$\overrightarrow{BD}$=(-3,2$\sqrt{2}$),
∴$\overrightarrow{AC}•\overrightarrow{BD}$=3×(-3)+2$\sqrt{2}$×2$\sqrt{2}$=-1,
故答案为:-1.
点评 本题考查了向量的数量积的运算,关键是建立坐标系,属于基础题.

练习册系列答案
相关题目
14.若变量x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x-3y≤9\\ x≥0\end{array}\right.$,则x2+2x+y2的最大值是( )
| A. | 4 | B. | 9 | C. | 16 | D. | 18 |
15.已知全集U=R,集合A={x||x|≤1},B={x|x≤1},则(∁UA)∩B等于( )
| A. | {x|x≤-1} | B. | {x|x<-1} | C. | {-1} | D. | {x|-1<x|≤1} |
13.复数z=$\frac{(1+i)(2-i)}{-i}$(i为虚数单位)的虚部为( )
| A. | -1 | B. | -i | C. | 3 | D. | 3i |