题目内容
17.已知定义域为I的函数f(x),若存在开区间(a,b)⊆I和正的常数c,使得任意x∈(a,b)都有-c<f(x)<c,且对任意x∉(a,b)都有|f(x)|=c恒成立,则称f(x)为区间I上的“Z型”函数,给出下列函数:①f(x)=$\left\{\begin{array}{l}{2,x≤1}\\{4-2x,1<x<3}\\{-2,x≥3}\end{array}\right.$;②f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{0,x<0}\end{array}\right.$;③f(x)=|sinx|;④f(x)=x+cosx,其中是区间I上的“Z型”函数的是①(只需写出序号即可)分析 ①根据题中的定义,逐步判断即可;
②④在x取无穷大时,函数值也为无穷大,③根据函数的图象显然可判断.
解答 解:①当x∈(1,3)时,f(x)=4-2x,则-2<f(x)<2;
当x∈[3,+∞)时,f(x)=-2,当x∈(-∞,1]时,f(x)=2,
∴|f(x)|=2;即满足对任意的x∈(1,3)都有-C<f(x)<C,
且对任意的x∉(1,3)都有|f(x)|=C恒成立,
即①为R上的“Z型”函数,故正确;
②④在x取无穷大时,函数值也为无穷大,
故不存在对任意的x∉(a,b)都有|f(x)|=C恒成立,故不是“Z型”函数,错误;
③根据函数的图象知函数为周期函数,虽然有最值,但不符合题中的条件,
不满足对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x∉(a,b)都有|f(x)|=C恒成立,
故错误.
故答案为:①.
点评 考查了对新定义函数的理解,紧扣定义,利用定义判断是否符合定义是关键.

练习册系列答案
相关题目
8.已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1的左、右焦点分别为F1、F2,且F2为抛物线y2=2px的焦点,设P为两曲线的一个公共点,则△PF1F2的面积为( )
| A. | 18 | B. | 18$\sqrt{3}$ | C. | 36 | D. | 36$\sqrt{6}$ |
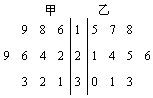 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.