Question

6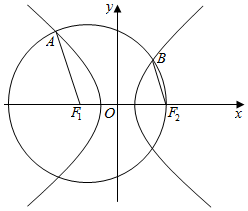．如图，设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，若以F₁为圆心，以F₁F₂为半径的圆与C交于A，B两点（A在第二象限，B在第一象限），且F₁A∥F₂B，则双曲线C的离心率为（　　）

• A． $\frac{3+\sqrt{17}}{4}$
• B． 2
• C． $\frac{1+\sqrt{17}}{4}$
• D． 3

Answer 1

分析 连接BF₁，AF₂，由双曲线的定义，可得|AF₂|=2a+2c，|BF₂|=2c-2a，在△AF₁F₂中，和△BF₁F₂中，运用余弦定理求得cos∠AF₁F₂，os∠BF₂F₁，由F₁A∥F₂B，可得∠BF₂F₁+∠AF₁F₂=π，即有cos∠BF₂F₁+cos∠AF₁F₂=0，化简整理，由离心率公式计算即可得到所求值．

解答 解：连接BF₁，AF₂，
由双曲线的定义，可得|AF₂|-|AF₁|=2a，
|BF₁|-|BF₂|=2a，
由|BF₁|=|AF₁|=2c，
可得|AF₂|=2a+2c，|BF₂|=2c-2a，
在△AF₁F₂中，可得cos∠AF₁F₂=$\frac{（2c）^{2}+（2c）^{2}-（2a+2c）^{2}}{2•2c•2c}$=$\frac{{c}^{2}-2ac-{a}^{2}}{2{c}^{2}}$，
在△BF₁F₂中，可得cos∠BF₂F₁=$\frac{（2c）^{2}+（2c-2a）^{2}-（2c）^{2}}{2•2c•（2c-2a）}$=$\frac{c-a}{2c}$，
由F₁A∥F₂B，可得∠BF₂F₁+∠AF₁F₂=π，即有cos∠BF₂F₁+cos∠AF₁F₂=0，
可得$\frac{{c}^{2}-2ac-{a}^{2}}{2{c}^{2}}$+$\frac{c-a}{2c}$=0，化为2c²-3ac-a²=0，
由e=$\frac{c}{a}$，可得2e²-3e-1=0，解得e=$\frac{3+\sqrt{17}}{4}$（负的舍去），
故选：A．

点评 本题考查双曲线的离心率的求法，注意运用双曲线的定义和三角形的余弦定理，考查化简整理的运算能力，属于中档题．