题目内容
14．函数f（x）=$\frac{lg（2-x）}{\sqrt{12+x-{x}^{2}}}$+（x-1）0的定义域为{x|-3＜x＜2且x≠1}．分析 根据函数f（x）的解析式，列出使函数解析式有意义的不等式组，求出解集即可．
解答 解：∵函数f（x）=$\frac{lg（2-x）}{\sqrt{12+x-{x}^{2}}}$+（x-1）0，
∴$\left\{\begin{array}{l}{2-x＞0}\\{12+x{-x}^{2}＞0}\\{x-1≠0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x＜2}\\{-3＜x＜4}\\{x≠1}\end{array}\right.$，
即-3＜x＜2且x≠1；
∴函数f（x）的定义域为{x|-3＜x＜2且x≠1}．
故答案为：{x|-3＜x＜2且x≠1}．
点评 本题考查了根据函数解析式求定义域的应用问题，是基础题目．
练习册系列答案
备战中考寒假系列答案
相关题目
2．已知y=f（x）为偶函数，且f（-3）=20，则f（3）=（ ）
| A． | 3 | B． | -3 | C． | 20 | D． | -20 |
19．复数z=$\frac{-i}{4+i}$（其中i为虚数单位）的虚部为（ ）
| A． | -$\frac{1}{17}$ | B． | $\frac{4}{17}$ | C． | -$\frac{4}{17}$i | D． | -$\frac{4}{17}$ |
6．
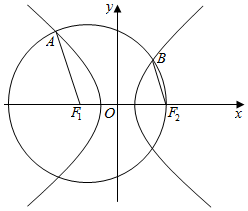如图，设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，若以F1为圆心，以F1F2为半径的圆与C交于A，B两点（A在第二象限，B在第一象限），且F1A∥F2B，则双曲线C的离心率为（ ）
如图，设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，若以F1为圆心，以F1F2为半径的圆与C交于A，B两点（A在第二象限，B在第一象限），且F1A∥F2B，则双曲线C的离心率为（ ）| A． | $\frac{3+\sqrt{17}}{4}$ | B． | 2 | C． | $\frac{1+\sqrt{17}}{4}$ | D． | 3 |