题目内容
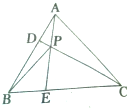如图所示，正三角形ABC中，D，E分别是AB，BC上的一个三等分点，且分别靠近点A、点B，且AE、CD交于点P．求证：BP⊥DC．考点：直线与平面垂直的性质
专题：平面向量及应用,空间位置关系与距离
分析：设正三角形ABC的边长为，6，取B为坐标原点，BC为x轴，BE=2．可求出B，A，D，E，C点的坐标．从而可得AE方程，CD方程，解得交点P（
，
），可求出BP斜率与CD斜率之积为-1，从而证明BP⊥DC．
| 18 |
| 7 |
12
| ||
| 7 |
解答：
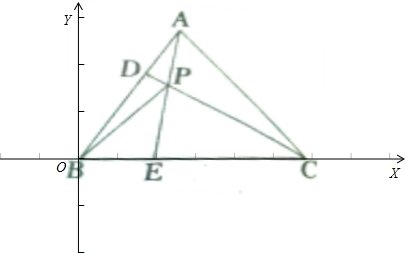解：设正三角形ABC的边长为，6，取B为坐标原点，BC为x轴，BE=2．
则有：B（0，0），A（3，3
），D（2，2
），E（2，0），C（6，0）．
AE方程：3
=
．
CD方程：
=
．
解得交点P（
，
）．
BP斜率=
=
．
CD斜率=
=-
．
∵
×（-
）=-1．
∴BP⊥CD
解：设正三角形ABC的边长为，6，取B为坐标原点，BC为x轴，BE=2．则有：B（0，0），A（3，3
| 3 |
| 3 |
AE方程：3
| 3 |
| y |
| x-2 |
CD方程：
2
| ||
| -4 |
| y |
| x-6 |
解得交点P（
| 18 |
| 7 |
12
| ||
| 7 |
BP斜率=
12
| ||
| 18 |
2
| ||
| 3 |
CD斜率=
2
| ||
| -4 |
| ||
| 2 |
∵
2
| ||
| 3 |
| ||
| 2 |
∴BP⊥CD
点评：本题主要考察了直线与平面垂直的性质，平面向量及应用，属于基本知识的考查．
练习册系列答案
优加精卷系列答案
相关题目
已知向量
=(1，0)与向量
=(1，
)，则向量
与
的夹角是（ ）
| a |
| b |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
方程|log2x-2|+1=|log2x|的解集是（ ）
| A、{2，8} | |||||
B、{2
| |||||
C、{
| |||||
D、{2，
|
自二面角α-l-β的棱l上任选一点O，若∠AOB是二面角α-l-β的平面角，必须具备条件（ ）
| A、AO⊥OB，AO?α，BO?β |
| B、AO⊥l，BO⊥l |
| C、AB⊥l，AO?α，BO?β |
| D、AO⊥l，OB⊥l，AO?α，BO?β |