题目内容
已知椭圆 的长轴长为10,离心率
的长轴长为10,离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )
 的长轴长为10,离心率
的长轴长为10,离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )A.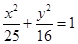 或 或 | B.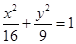 或 或 |
C. 或 或 | D.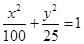 或 或 |
A
试题分析:因为由题意可知椭圆
 的长轴长为10,离心率
的长轴长为10,离心率 ,可知2a=10,a=5,同时
,可知2a=10,a=5,同时 ,那么结合
,那么结合 ,由于焦点位置不确定,因此可知其方程有两种情况,故可知为
,由于焦点位置不确定,因此可知其方程有两种情况,故可知为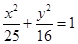 或
或 ,进而选A.
,进而选A.点评:解决该试题的关键是先根据题意求得a,进而根据离心率求得c,则根据a,b和c的关系求得b,则椭圆的方程可得.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
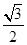 的椭圆
的椭圆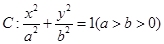 过点
过点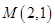 ,
,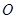 为坐标原点,平行于
为坐标原点,平行于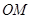 的直线
的直线 交椭圆于
交椭圆于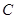 不同的两点
不同的两点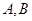 。
。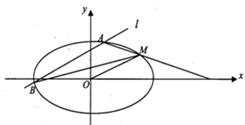
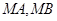 的斜率分别为
的斜率分别为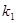 、
、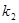 ,求证:
,求证: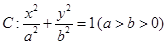 .
.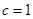 ,且
,且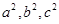 成等差数列,求椭圆
成等差数列,求椭圆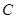 的方程;
的方程;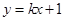 相交于
相交于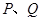 两点,求
两点,求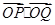 的取值范围.
的取值范围.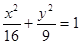 的两焦点是
的两焦点是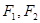 ,则其焦距长为 ,若点
,则其焦距长为 ,若点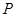 是椭圆上一点,且
是椭圆上一点,且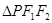 是直角三角形,则
是直角三角形,则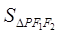 的大小是 .
的大小是 .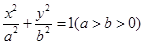 的上顶点坐标为
的上顶点坐标为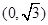 ,离心率为
,离心率为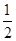 .
.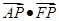 的取值范围.
的取值范围.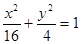 上有两点P、Q ,O为原点,若OP、OQ斜率之积为
上有两点P、Q ,O为原点,若OP、OQ斜率之积为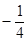 ,
,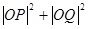 等于( )
等于( )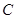 过点
过点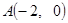 ,且与圆
,且与圆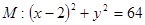 相内切,则动圆
相内切,则动圆 的离心率为
的离心率为 ,焦点在x轴上且长轴长为30.若曲线
,焦点在x轴上且长轴长为30.若曲线 上的点到椭圆
上的点到椭圆



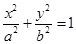 (
(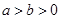 )的左焦点
)的左焦点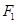 作
作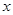 轴的垂线交椭圆于点
轴的垂线交椭圆于点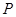 ,
,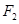 为右焦点,若
为右焦点,若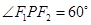 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


