题目内容
设m、n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,n∥α,则m∥n
④若α⊥γ,β⊥γ,则α∥β
其中正确命题的个数是( )
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,n∥α,则m∥n
④若α⊥γ,β⊥γ,则α∥β
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系判断.
解答:
解:由m、n是两条不同的直线,α,β,γ是三个不同的平面,知:
①若m⊥α,n∥α,则由直线与平面垂直的性质知m⊥n,故①正确;
②若α∥β,β∥γ,m⊥α,
则由平面与平面平行的判定定理和直线与平面垂直的判定定理知m⊥γ,故②正确;
③若m∥α,n∥α,则m与n相交、平行或异面,故③错误;
④若α⊥γ,β⊥γ,则α与β相交或平行,故④错误.
故选:B.
①若m⊥α,n∥α,则由直线与平面垂直的性质知m⊥n,故①正确;
②若α∥β,β∥γ,m⊥α,
则由平面与平面平行的判定定理和直线与平面垂直的判定定理知m⊥γ,故②正确;
③若m∥α,n∥α,则m与n相交、平行或异面,故③错误;
④若α⊥γ,β⊥γ,则α与β相交或平行,故④错误.
故选:B.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
函数y=a(x+2)+1的图象过定点( )
| A、(1,2) |
| B、(2,1) |
| C、(-2,2) |
| D、(-1,1) |
函数y=
的大致图象如图所示,则( )

| x |
| x2+a |

| A、a∈(-1,0) |
| B、a∈(0,1) |
| C、a∈(-∞,1) |
| D、a∈(1,+∞) |
函数y=2|x|的值域为( )
| A、(0,1) |
| B、(0,1] |
| C、(0,+∞) |
| D、[1,+∞) |
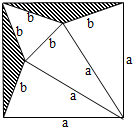 如图,把边长为a的正方形剪去图中的阴影部分,沿图中所画的折成一个正三棱锥,则这个正三棱锥的高是( )
如图,把边长为a的正方形剪去图中的阴影部分,沿图中所画的折成一个正三棱锥,则这个正三棱锥的高是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
和两条异面直线都平行的直线( )
| A、只有一条 | B、两条 |
| C、无数条 | D、不存在 |
下列关系式中正确的是( )
| A、sin10°<cos10°<sin160° |
| B、sin160°<sin10°<cos10° |
| C、sin10°<sin160°<cos10° |
| D、sin160°<cos10°<sin10° |