题目内容
已知A是三角形ABC的内角，则“cosA=
”是“sinA=
”的（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据三角函数的公式，利用充分条件和必要条件的定义进行判断．
解答：
解：∵A是三角形ABC的内角，
∴若cosA=
，则A=
，此时sinA=
成立，即充分性成立．
若sinA=
，则A=
或
，当A=
，cosA=-
，即必要性不成立，
故“cosA=
”是“sinA=
”充分不必要条件，
故选：A．
∴若cosA=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
若sinA=
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
故“cosA=
| 1 |
| 2 |
| ||
| 2 |
故选：A．
点评：本题主要考查充分条件和必要条件的应用，根据三角函数的关系式是解决本题的关键．
练习册系列答案
相关题目
数列{an}满足an=
，则该数列从第5项到第15项的和为（ ）
|
| A、2016 | B、1528 |
| C、1504 | D、992 |
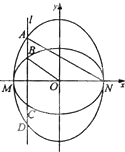如图，已知椭圆C1的中心在原点O，长轴左、右端点M，N在x轴上，椭圆C2的短轴为MN，且C1，C2的离心率都为e，直线l⊥MN，l与C1交于两点，与C2交于两点，这四点按纵坐标从大到小依次为A，B，C，D，且BO∥AN，则离心率e的范围是（ ）A、
| ||||
B、0＜e＜
| ||||
C、0＜e＜
| ||||
D、
|
下列函数中值域是（0，+∞）的是（ ）
A、y=
| ||
B、y=x2+x+
| ||
| C、y=2x | ||
| D、y=2x+1 |
等比数列{an}的公比为q，其前n项积为Tn，且满足a1＞1，a99•a100-1＞0，
＜0．得出下列结论：（1）0＜q＜1；（2）a99•a100-1＜0；（3）T100的值是Tn中最大的；（4）使Tn＞1成立的最大自然数n等于198．其中正确的结论的个数为（ ）
| a99-1 |
| a100-1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
复数z=
（i为虚数单位），则z的共轭复数
是（ ）
| 1 |
| 1+i |
. |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中，AB=6，BC=3，AC=5，则
•
=（ ）
| AB |
| BC |
| A、10 | B、-12 |
| C、-10 | D、20 |