题目内容
已知函数f（x）=x2-2x+3，x∈[-1，4]，则函数f（x）的值域为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：利用函数的解析式，确定函数的对称轴和图象的开口方向，运用二次函数的性质，即可求得函数f（x）的值域．
解答：
解：∵函数f（x）=x2-2x+3，
∴f（x）=（x-1）2+2，
对称轴为x=1，图象是开口向上的抛物线，
∵离对称轴越近，其对应的函数值越小，
又∵x∈[-1，4]，
∴当x=1时，f（x）取得最小值为2，
当x=4时，f（x）取得最大值为11，
∴f（x）的值域为[2，11]．
故答案为：[2，11]．
∴f（x）=（x-1）2+2，
对称轴为x=1，图象是开口向上的抛物线，
∵离对称轴越近，其对应的函数值越小，
又∵x∈[-1，4]，
∴当x=1时，f（x）取得最小值为2，
当x=4时，f（x）取得最大值为11，
∴f（x）的值域为[2，11]．
故答案为：[2，11]．
点评：本题考查了二次函数的性质以及求函数的值域问题．求函数的值域要注意考虑定义域的取值，再根据函数的解析式进行判断该使用何种方法求解值域．对于二次函数的最值，一般要注意考虑开口方向和对称轴与区间的位置关系，用离对称轴的远近来判断哪一个值取得最大值和最小值．属于基础题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
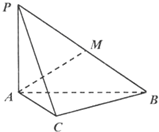如图，三棱锥P-ABC中，∠ACB=90°，PA⊥底面ABC．在直角坐标系中，直线x+
y-3=0的斜率是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|