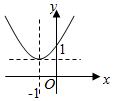题目内容
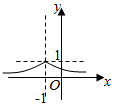
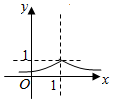
1.如图所示,函数y=cosx•$\frac{|sinx|}{|cosx|}$(0≤x<$\frac{3π}{2}$且x≠$\frac{π}{2}$)的图象是( )| A. |  | B. |  | C. | 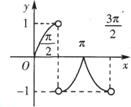 | D. | 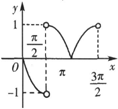 |
分析 根据解析式可知f(x)的符号与cosx的符号一致,故可根据x的象限判断f(x)的符号得出答案.
解答 解:当0<x<$\frac{π}{2}$,f(x)=cosx$•\frac{sinx}{cosx}$=sinx>0,
当$\frac{π}{2}$<x<π时,f(x)=cosx$•\frac{sinx}{-cosx}$=-sinx<0,
当π<x<$\frac{3π}{2}$时,f(x)=cosx•$\frac{-sinx}{-cosx}$=sinx<0,
故选C.
点评 本题考查了三角函数化简,三角函数的图象,属于基础题.

练习册系列答案
相关题目
12.执行如图所示的程序框图,输出的S值为( )


| A. | 6 | B. | 10 | C. | 14 | D. | 15 |
16.将[0,1]内的均匀随机数转化为[-3,4]内的均匀随机数,需要实施的变换( )
| A. | a=a1*7 | B. | a=a1*7+3 | C. | a=a1*7-3 | D. | a=a1*4 |
13.在复平面内,复数$\frac{2}{1-i}$+2i2对应的点与原点的距离是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |