题目内容
9.求y=cos2x-sinx-3的值域.分析 由三角函数知识化简函数的表达式为正弦函数的形式,令sinx=t,则t∈[-1,1],利用二次函数的性质求解函数值域即可.
解答 解:化简可得y=cos2x-sinx-3=-sin2x-sinx-2
=-(sinx-$\frac{1}{2}$)2-$\frac{7}{4}$,
令sinx=t,则t∈[-1,1],
由二次函数的性质可知y=-2(t-$\frac{1}{2}$)2-$\frac{7}{4}$,
在t∈[-1,$\frac{1}{2}$]单调递增,在t∈[$\frac{1}{2}$,1]单调递减,
∴当t=$\frac{1}{2}$时,函数取到最大值:$-\frac{7}{4}$,
当t=-1时,函数取到最小值-2.
y=cos2x-sinx-3的值域:[-2,-$\frac{7}{4}$].
点评 本题考查复合三角函数的单调性和最值,换元是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.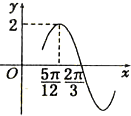 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{1}{12}$π] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] |
20.已知函数f(x)=2sinx的定义域为[a,b],值域为[-1,2],则b-a的值不可能是( )
| A. | $\frac{2π}{3}$ | B. | π | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
14.对任意的m∈(-1,4),直线l:x+4y+m(x-y)-1=0与坐标轴围成的三角形的面积小于$\frac{1}{8}$的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |