题目内容
 已知棱柱ABCD-A′B′C′D′,底面ABCD是边长为a的菱形,∠BAD=60°,对角线AC、BD交于点O,A′O⊥平面ABCD.
已知棱柱ABCD-A′B′C′D′,底面ABCD是边长为a的菱形,∠BAD=60°,对角线AC、BD交于点O,A′O⊥平面ABCD.(Ⅰ)证明:不论侧棱AA′的长度为何值,总有平面AA′C′C⊥平面BB′D′D;
(Ⅱ)当二面角B-DD′-C为45°时,求侧棱AA′的长度.
考点:直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(I)分别以OA,OB,OA′为x,y,z轴建立空间直角坐标系O-xyz,求出平面AA′C′C的一个法向量和平面BB′D′D的法向量,根据两个平面的法向量垂直得到不论侧棱AA′的长度为何值,总有平面AA′C′C⊥平面BB′D′D;
(Ⅱ)求出平面CDD′C′的法向量,结合二面角B-DD′-C为45°,求出h与a的关系,进而利用勾股定理可得侧棱AA′的长度.
(Ⅱ)求出平面CDD′C′的法向量,结合二面角B-DD′-C为45°,求出h与a的关系,进而利用勾股定理可得侧棱AA′的长度.
解答:
证明:(Ⅰ)∵ABCD为菱形,
∴AC⊥BD,
又A′O⊥平面ABCD,
∴A′O⊥BD,A′O⊥AC,
分别以OA,OB,OA′为x,y,z轴建立空间直角坐标系O-xyz,
∵底面ABCD是边长为a的菱形,∠BAD=60°,
∴A(
,0,0),B(0,
,0).D(0,-
,0),
设OA′=h,则A′(0,0,h).
显然,平面AA′C′C的一个法向量为
=(0,1,0),
设平面BB′D′D的法向量为
=(x,y,z),
由
=(0,a,0),
=
=(-
,0,h),
得:
,即
,
取x=1,则
=(1,0,
),
则
•
=0,
即平面AA′C′C⊥平面BB′D′D,
故不论侧棱AA′的长度为何值,总有平面AA′C′C⊥平面BB′D′D.
解:(Ⅱ)设平面CDD′C′的法向量为
=(x,y,z),
由
=
=(-
,
,0).
=
=(-
,0,h),
得:
,即
,
取x=1,则
=(1,
,
),
则cos<
,
>=
=
,
又二面角B-DD′-C为45°,所以cos<
,
>=
,
=
,解得h2=
,
此时AA′=
=
=
a.
∴AC⊥BD,
又A′O⊥平面ABCD,
∴A′O⊥BD,A′O⊥AC,
分别以OA,OB,OA′为x,y,z轴建立空间直角坐标系O-xyz,
∵底面ABCD是边长为a的菱形,∠BAD=60°,
∴A(
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
设OA′=h,则A′(0,0,h).
显然,平面AA′C′C的一个法向量为
| m |
设平面BB′D′D的法向量为
| n |
由
| DB |
| BB′ |
| AA′ |
| ||
| 2 |
|
|
|
取x=1,则
| n |
| ||
| 2h |
则
| m |
| n |
即平面AA′C′C⊥平面BB′D′D,
故不论侧棱AA′的长度为何值,总有平面AA′C′C⊥平面BB′D′D.
解:(Ⅱ)设平面CDD′C′的法向量为
| p |
由
| DC |
| AB |
| ||
| 2 |
| a |
| 2 |
| DD′ |
| AA′ |
| ||
| 2 |
|
|
|
取x=1,则
| p |
| 3 |
| ||
| 2h |
则cos<
| n |
| p |
1+
| ||||||||
|
| ||||
|
又二面角B-DD′-C为45°,所以cos<
| n |
| p |
| ||
| 2 |
| ||||
|
| ||
| 2 |
| 3a2 |
| 8 |
此时AA′=
| h2+OA2 |
|
3
| ||
| 4 |
点评:本题考查的知识点是直线与平面垂直的判定,二面角,平面与平面垂直的判定,其中建立空间坐标系,将面面垂直问题和二面角问题,转化为向量垂直和向量夹角问题是解答的关键.

练习册系列答案
相关题目
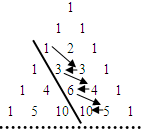 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为