题目内容
已知sinβ=
,(
<β<π),且sin(α+β)=cosα,则tan(α+β)=( )
| 3 |
| 5 |
| π |
| 2 |
| A、1 | ||
| B、2 | ||
| C、-2 | ||
D、
|
考点:两角和与差的正切函数
专题:计算题,三角函数的求值
分析:利用sin(α+β)=cos(α+β)cosβ+sin(α+β)sinβ,即可求出tan(α+β).
解答:
解:∵sinβ=
,(
<β<π),
∴cosβ=-
,
∵sin(α+β)=cosα,
∴sin(α+β)=cos(α+β)cosβ+sin(α+β)sinβ,
∴sin(α+β)=-
cos(α+β)+
sin(α+β),
∴
sin(α+β)=-
cos(α+β),
∴tan(α+β)=-2.
故选:C.
| 3 |
| 5 |
| π |
| 2 |
∴cosβ=-
| 4 |
| 5 |
∵sin(α+β)=cosα,
∴sin(α+β)=cos(α+β)cosβ+sin(α+β)sinβ,
∴sin(α+β)=-
| 4 |
| 5 |
| 3 |
| 5 |
∴
| 2 |
| 5 |
| 4 |
| 5 |
∴tan(α+β)=-2.
故选:C.
点评:本题考查角的变换,考查学生的计算能力,利用sin(α+β)=cos(α+β)cosβ+sin(α+β)sinβ是关键.

练习册系列答案
相关题目
已知直线l与过点M(-
,
)、N(
,-
)的直线垂直,则直线l的倾斜角是( )
| 3 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)=
,则∫
f(x)dx=( )
|
2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知p:|2x-3|<1,q:x(x-3)<0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=lnx+2x-6的零点属于区间(n,n+1)(n∈z),则n等于( )
| A、1 | B、2 | C、3 | D、4 |
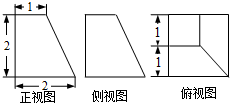 已知台体的体积公式V=
已知台体的体积公式V=