Question

13．若函数y=f（x）同时满足：（ⅰ）对于定义域内的任意x，恒有f（x）+f（-x）=0；（ⅱ）对于定义域内的任意x₁，x₂，当x₁≠x₂时，恒有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＜0$，则称函数f（x）为“二维函数”．现给出下列四个函数：
①f（x）=$\frac{1}{x}$
②f（x）=-x³+x
③$f（x）={log_{\frac{1}{2}}}x$
④$f（x）=\left\{\begin{array}{l}-{x^2}，x≥0\\{x^2}，x＜0\;.\end{array}\right.$
其中能被称为“二维函数”的有④（写出所有满足条件的函数的序号）．

Answer 1

分析 由（i）可知f（x）是奇函数，由（ii）可知f（x）定义域上的减函数，逐个分析每个函数的奇偶性和单调性即可．

解答 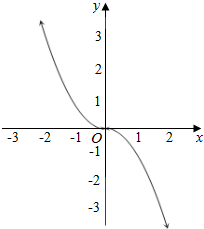解：由（i）可知f（x）是奇函数，由（ii）可知f（x）定义域上的减函数．
对于①，f（x）=$\frac{1}{x}$在定义域上不单调，不符合条件（ii），
对于②，f（x）=-x³+x在R上不单调，不符合条件（ii），
对于③，f（x）=log${\;}_{\frac{1}{2}}$x不是奇函数，不符合条件（i），
对于④，作出f（x）的函数图象，由图象可知$f（x）=\left\{\begin{array}{l}-{x^2}，x≥0\\{x^2}，x＜0\;.\end{array}\right.$是奇函数，且在R上是减函数．
故答案为④．

点评 本题考查了函数奇偶性和单调性的判断，属于中档题．