题目内容
12．己知函数f（x）=ex+ax2-x+1，a≥0，求f（x）的单调区间．分析 求出f（x）的导数，得到f′（x）在R递增，结合f′（0）=0，从而求出函数的单调区间．
解答 解：函数f（x）=ex+ax2-x+1，a≥0，
∴f′（x）=ex+2ax-1，
∴f″（x）=ex+2a＞0，
∴f′（x）在R递增，
而f′（0）=0，
∴x＜0时，f′（x）＜0，x＞0时，f′（x）＞0，
∴f（x）在（-∞，0）递减，在（0，+∞）递增．
点评 本题考查了求函数的单调性问题，考查导数的应用，求出导函数的单调性是解题的关键，本题是一道中档题．
练习册系列答案
阅读快车系列答案
相关题目
2．
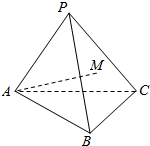如图，在三棱锥P-ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（ ）
如图，在三棱锥P-ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{6}{7}$ | D． | $\frac{4\sqrt{3}}{7}$ |
3．已知函数f（x）=sin（ωx+φ）对任意的x∈R满足f（x）≤|f（$\frac{π}{4}$）|，若函数g（x）=cos（ωx+φ）-1，则g（$\frac{π}{4}$）的值为（ ）
| A． | -3 | B． | 1 | C． | -1 | D． | 1或-3 |
20．
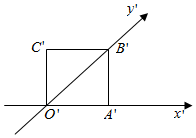如图，正方形O′A′C′B′的边长为1cm，它是水平放置的一个平面图形的直观图，则它的原图形面积和直观图面积之比是（ ）
如图，正方形O′A′C′B′的边长为1cm，它是水平放置的一个平面图形的直观图，则它的原图形面积和直观图面积之比是（ ）| A． | 2$\sqrt{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | 2（1+$\sqrt{3}$） | D． | 6 |
17．已知函数f（x）=xn的图象过点（3，$\sqrt{3}$），则n=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
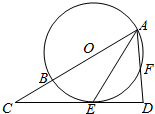如图所示，⊙O的圆心O在Rt△ACD的斜边AC上，且⊙O过顶点A，与边CD相切于点E，与边AD、AC分别相交于点F，B．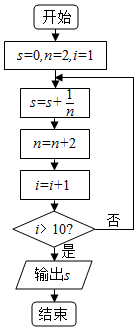
已知函数f（x）=2sin（ωx+$\frac{π}{4}$）在一个周期内的图象如图所示．