题目内容
如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为________cm3.

6
[解析] 本题考查长方体及四棱锥体积等知识,考查空间想象能力.
连接AC交BD于O点,∵AB=AD,
∴四边形ABCD为正方形,∴AO⊥BD.
在长方体ABCD-A1B1C1D1中,B1B⊥面ABCD,
又AO面ABCD,∴B1B⊥AO.
又B1B∩BD=B,∴AO⊥面B1BDD1,
即AO长为四棱锥A-B1BDD1的高,
∴AO= =
=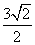 ,S矩B1BDD1=BB1×BD=3
,S矩B1BDD1=BB1×BD=3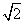 ×2=6
×2=6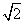 .
.
∴VA-BB1D1D=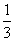 S矩BB1D1D×AD=
S矩BB1D1D×AD=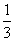 ×6
×6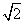 ×
×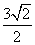 =6.
=6.

练习册系列答案
相关题目
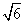 π B.4
π B.4 π
π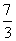 πa2
πa2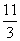 πa2 D.5πa2
πa2 D.5πa2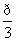 ,则cos<
,则cos<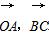 >的值为( )
>的值为( )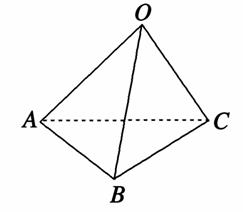
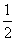
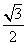 D.
D.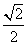
 .
.