题目内容
8.在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x-y+1=0和x+y-7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(-m,0)(m,0),则m的最大值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 求出⊙C的方程,过P,M,N的圆的方程,两圆外切时,m取得最大值.
解答 解:由题意,∴A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x-y+1=0和x+y-7=0,
∴圆上不相同的两点为B(2,4,),D(4,4),
∵A(3,3),BA⊥DA
∴BD的中点为圆心C(3,4),半径为1,
∴⊙C的方程为(x-3)2+(y-4)2=1.
过P,M,N的圆的方程为x2+y2=m2,
∴两圆外切时,m的最大值为$\sqrt{{4}^{2}+{3}^{2}}$+1=6,
故选:C.
点评 本题考查圆的方程,考查圆与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
20.不等式组$\left\{\begin{array}{l}{x>0}\\{x+y<3}\\{y>x+1}\end{array}\right.$表示的平面区域为M,直线y=kx-1与区域M没有公共点,则实数k的最大值为( )
| A. | 3 | B. | 0 | C. | -3 | D. | 不存在 |
18.已知sin($\frac{2015}{2}$π+α)=$\frac{1}{5}$,那么cosα=( )
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -1 | D. | 1 |
 有一个容量为n的样本,其频率分布直方图如图所示,已知样本数据在区间[10,12)内的频数为18,则实数n=100.
有一个容量为n的样本,其频率分布直方图如图所示,已知样本数据在区间[10,12)内的频数为18,则实数n=100.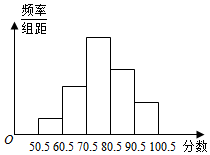 从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:
从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题: