题目内容
16.讨论f(x)=ex-ax的单调性.分析 由导函数f′(x)知,需要对a进行分类讨论.a≤0和a>0的情形.再由导函数的正负,确定原函数的增减性.
解答 解:∵f(x)=ex-ax
∴f′(x)=ex-a
①a≤0时,f′(x)>0,f(x)在R上单调递增
②a>0时,由f′(x)=0得:x=lna
x∈(-∞,lna)时,f′(x)<0,f(x)是单调递减的.
x∈(lna,+∞)时,f′(x)>0,f(x)是单调递增的.
综上所述:a≤0时,f(x)在R上单调递增,
a>0时,f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
点评 本题考查函数求导与分类讨论思想.

练习册系列答案
相关题目
7.已知y=f(x)是定义在R上的偶函数,在区间[0,+∞)上单调递增,且f(1)=0,那么不等式$\frac{f(x)}{x}$>0的解集是( )
| A. | {x|x>1或-1<x<0} | B. | {x|x>1或x<-1} | C. | {x|0<x<1或x<-1} | D. | {x|-1<x<1且x≠0} |
4.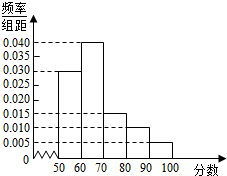 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )| A. | 0.004 | B. | 0.04 | C. | 0.4 | D. | 4 |
1.设集合P={0,1,2},N={x|x2-3x+2=0},则P∩(∁RN)=( )
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | 以上答案都不对 |
5.已知α∈(π,$\frac{3π}{2}$),sinα=-$\frac{3}{5}$,则cosα等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{5}$ |
6.已知三棱锥P-ABC的四个顶点都在球O的球面上,△ABC是边长为2$\sqrt{3}$的正三角形,PA⊥平面ABC,若三棱锥P-ABC的体积为2$\sqrt{3}$,则球O的表面积为( )
| A. | 18π | B. | 20π | C. | 24π | D. | 20$\sqrt{3}$π |