题目内容
20．不等式组$\left\{\begin{array}{l}{x＞0}\\{x+y＜3}\\{y＞x+1}\end{array}\right.$表示的平面区域为M，直线y=kx-1与区域M没有公共点，则实数k的最大值为（ ）| A． | 3 | B． | 0 | C． | -3 | D． | 不存在 |
分析 作出不等式组对应的平面区域，利用线性规划的知识即可得到结论．
解答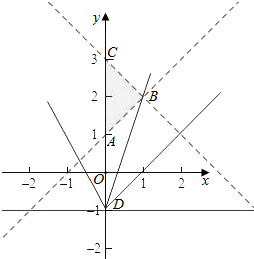 
解：直线y=kx-1过定点D（0，-1）
作出不等式组对应的平面区域如图：
当k≤0时，直线y=kx-1与区域M没有公共点，
当k＞0时，要使直线y=kx-1与区域M没有公共点，
要使k最大此时直线y=kx-1经过B时，满足条件．
由$\left\{\begin{array}{l}{x+y=3}\\{y=x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，即B（1，2），
此时点B在直线y=kx-1上，
则k-1=2，得k=3，
即要使直线y=kx-1与区域M没有公共点，
则k≤3，
即实数k的最大值为3，
故选：A．
点评 本题主要考查线性规划以及斜率的应用，结合直线的斜率，利用数形结合是解决本题的关键．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5．已知α∈（π，$\frac{3π}{2}$），sinα=-$\frac{3}{5}$，则cosα等于（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | -$\frac{1}{7}$ | D． | -$\frac{4}{5}$ |
9．若正实数a，b满足a+2b=1，则下列说法正确的是（ ）
| A． | ab有最大值$\frac{1}{4}$ | B． | $\frac{1}{a}$+$\frac{1}{b}$有最小值5 | ||
| C． | $\sqrt{a}$+$\sqrt{2b}$有最大值1+$\sqrt{2}$ | D． | a2+4b2有最小值$\frac{1}{2}$ |
10．某企业上半年产品产量与单位成本资料如表：
且已知产量x与成本y具有线性相关关系（a，b用小数表示，结果精确到0.01）．
（1）求出y关于x的线性回归方程（给出数据$\sum_{i=1}^{n}$xiyi=1481）；
（2）指出产量每增加1000件时，单位成本平均变动多少？
（3）假定产量为6000件时，单位成本为多少元？
| 月份 | 产量（千件） | 单位成本（元） |
| 1 | 2 | 73 |
| 2 | 3 | 72 |
| 3 | 4 | 71 |
| 4 | 3 | 73 |
| 5 | 4 | 69 |
| 6 | 5 | 68 |
（1）求出y关于x的线性回归方程（给出数据$\sum_{i=1}^{n}$xiyi=1481）；
（2）指出产量每增加1000件时，单位成本平均变动多少？
（3）假定产量为6000件时，单位成本为多少元？