题目内容
17.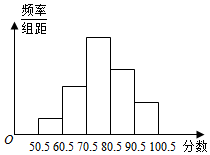 从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:
从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:(1)求样本容量;
(2)若从第3,4,5组中采用分层抽样的方法抽取6人参加竞赛成绩分析会,求从第3,4,5组中各抽取的学生人数.
分析 (1)根据最右边一组的频数是6,而频率等于该组的面积在整个图形面积中的百分比,因此可得样本容量为48;
(2)根据分层抽样,即可求出各小组的人数.
解答 解:在频率分布直方图中,长方形的高之比=面积之比=频数之比=频率之比
(1)∵最右边一组的频数是6,从左到右各小组的长方形的高之比为1:3:6:4:2
∴设样本容量为n,得(1+3+6+4+2):n=2:6
∴n=48,样本容量为48,
(2)第3组抽取的人数为6×$\frac{6}{6+4+2}$=2,
第4组抽取的人数为6×$\frac{4}{6+4+2}$=3,
第5组抽取的人数为6×$\frac{2}{6+4+2}$=1,
点评 本题考查了频率直方图的有关知识以及分层抽样,属于基础题.频率直方图中,各个小长方形的面积等于该组数据的频率,所有长方形的面积之和等于1.

练习册系列答案
相关题目
7.已知y=f(x)是定义在R上的偶函数,在区间[0,+∞)上单调递增,且f(1)=0,那么不等式$\frac{f(x)}{x}$>0的解集是( )
| A. | {x|x>1或-1<x<0} | B. | {x|x>1或x<-1} | C. | {x|0<x<1或x<-1} | D. | {x|-1<x<1且x≠0} |
5.已知α∈(π,$\frac{3π}{2}$),sinα=-$\frac{3}{5}$,则cosα等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{5}$ |
2.设等差数列{an}的前n项和为Sn,若a1=-40,a6+a10=-10,则当Sn取最小值时,n的值为( )
| A. | 8或9 | B. | 9 | C. | 8 | D. | 7 |
9.若正实数a,b满足a+2b=1,则下列说法正确的是( )
| A. | ab有最大值$\frac{1}{4}$ | B. | $\frac{1}{a}$+$\frac{1}{b}$有最小值5 | ||
| C. | $\sqrt{a}$+$\sqrt{2b}$有最大值1+$\sqrt{2}$ | D. | a2+4b2有最小值$\frac{1}{2}$ |
6.已知三棱锥P-ABC的四个顶点都在球O的球面上,△ABC是边长为2$\sqrt{3}$的正三角形,PA⊥平面ABC,若三棱锥P-ABC的体积为2$\sqrt{3}$,则球O的表面积为( )
| A. | 18π | B. | 20π | C. | 24π | D. | 20$\sqrt{3}$π |