题目内容
10.O是△ABC所在平面上一点,且$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$,|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{OC}$|,则∠C=30°.分析 由向量式可得O为边BC的中点,由等边三角形和等腰三角形的内角和可得.
解答 解:∵O是△ABC所在平面上一点,且$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$,
∴O为边BC的中点,又|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=|$\overrightarrow{OC}$|,
∴△ABO为等边三角形,故∠AOC=120°,
在等腰三角形AOC中易得∠C=30°,
故答案为:30°.
点评 本题考查向量的运算性质和几何意义,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,点
,点 是
是 边上的动点,点
边上的动点,点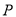 关于直线
关于直线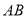 ,
, 的对称点分别为
的对称点分别为 ,则线段
,则线段 长的取值范围是 .
长的取值范围是 .
 ,记
,记 .
.  ,求
,求 的值;
的值;  中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.