题目内容
15.设全集U=R,集合A={x||x-4|≤2},B={x|x≥5},则A∩(∁UB)={x|2≤x<5}.分析 通过解绝对值不等式便可得出集合A={x|2≤x≤6},且B={x|x≥5},这样进行补集和交集的运算便可求出A∩(∁UB)的值.
解答 解:解|x-4|≤2得,2≤x≤6;
∴A={x|2≤x≤6},且∁UB={x|x<5};
∴A∩(∁UB)={x|2≤x<5}.
故答案为:{x|2≤x<5}.
点评 考查绝对值不等式的解法,以及集合的补集和交集的运算,描述法表示集合的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
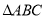 中,
中,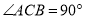 ,
,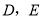 分别为
分别为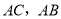 的中点,
的中点,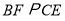 交
交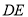 的延长线于点
的延长线于点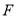 .
.
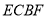 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形 ,且满足
,且满足 ,则
,则 的大小关系是_____________.
的大小关系是_____________.