题目内容
10.函数f(x)=$\frac{{x}^{2}+1}{x}$的奇偶性为( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
分析 首先明确函数的定义域,然后根据函数奇偶性的定义进行判断.
解答 解:函数的定义域为{x|x≠0},又f(-x)=$\frac{(-x)^{2}+1}{-x}$=-$\frac{{x}^{2}+1}{x}$=-f(x),所以函数为奇函数;
故选:A.
点评 本题考查了函数奇偶性的判定;两个步骤:①求定义域;在函数定义域关于原点对称的前提下②判定f(-x)与f(x)的关系;相等为偶函数;相反为奇函数.

练习册系列答案
相关题目
20.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2+c2-a2=bc,$\overrightarrow{AB}$•$\overrightarrow{BC}$>0,a=$\frac{\sqrt{3}}{2}$,则b+c的取值范围是( )
| A. | (1,$\frac{3}{2}$) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$] |
1.若关于x的不等式|x+1|-|x-2|<a2-4a有实数解,则实数a的取值范围是( )
| A. | a<1或a>3 | B. | a>3 | C. | a<1 | D. | 1<a<3 |
15.若函数y=sin2x+acos2x的图象关于直线x=-$\frac{π}{8}$对称,则a=( )
| A. | $-2-2\sqrt{2}$ | B. | $-2+2\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | -1 |
19.设an=-n2+9n+10,则数列{an}前n项和最大值n的值为( )
| A. | 4 | B. | 5 | C. | 9或10 | D. | 4或5 |
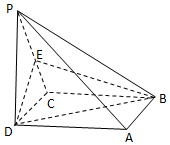 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点, 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为$\frac{4}{3}$.
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为$\frac{4}{3}$.