题目内容
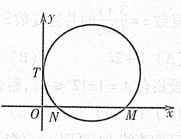
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N (点M在点N的右侧),且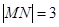 。椭圆D:
。椭圆D: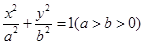 的焦距等于
的焦距等于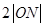 ,且过点
,且过点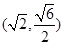
( I ) 求圆C和椭圆D的方程;
(Ⅱ) 若过点M的动直线 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线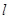 斜率的范围。
斜率的范围。
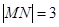 。椭圆D:
。椭圆D: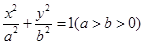 的焦距等于
的焦距等于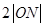 ,且过点
,且过点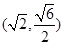

( I ) 求圆C和椭圆D的方程;
(Ⅱ) 若过点M的动直线
 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线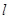 斜率的范围。
斜率的范围。(1)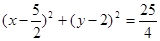 ,
,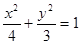
(2)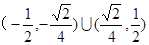
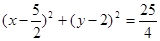 ,
,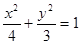
(2)
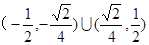
试题分析:)解:(1)设圆半径为r, 由条件知圆心C(r,2)
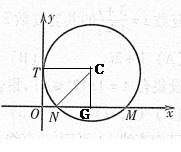
∵圆在x轴截得弦长MN=3
∴
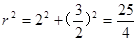 ∴r=
∴r=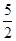
∴圆C的方程为:
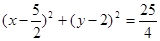 (3分)
(3分)上面方程中令y=0,得
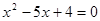 解得x=1或x="4," ∵点M在点N的右侧
解得x=1或x="4," ∵点M在点N的右侧∴M(4,0),N(1,0)
∵椭圆焦距2c=2
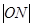 =2 ∴c=1 ∴椭圆方程可化为:
=2 ∴c=1 ∴椭圆方程可化为: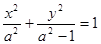
又椭圆过点(
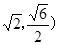 代入椭圆方程得:
代入椭圆方程得: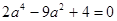
解得
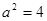 或
或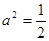 (舍) ∴椭圆方程为:
(舍) ∴椭圆方程为: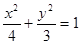 (6分)
(6分)(2)设直线l的方程为:y="k(x-4)" 代入椭圆方程化简得:
(
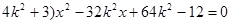
△=32
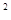
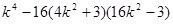 >0
>0 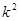 <
<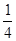
设A(x1,y1),B(x2,y2) 则x1+x2=
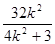 x1x2=
x1x2=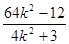 (7分)
(7分)∵点N在以弦AB为直径的圆的外部,
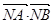 >0
>0∴(
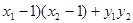 >0
>0即:
 >0
>0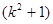
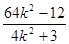 -(
-(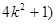
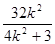 +
+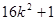 >0
>0化简得:
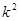 >
>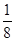 ∴
∴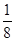 <
<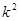 <
<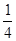 ∴k∈
∴k∈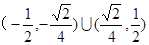
点评:主要是考查了圆的方程,以及椭圆性质的运用,并联立方程组设而不求的数学思想的运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,焦距的一半为3的椭圆的标准方程是( )
,焦距的一半为3的椭圆的标准方程是( )



 =1的两条渐近线互相垂直,那么该双曲线的离心率是 .
=1的两条渐近线互相垂直,那么该双曲线的离心率是 .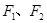 分别是双曲线
分别是双曲线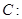
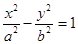 的左、右焦点,若
的左、右焦点,若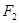 关于渐近线的对称点恰落在以
关于渐近线的对称点恰落在以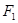 为圆心,
为圆心,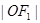 为半径的圆上,则
为半径的圆上,则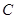 的离心率为( )
的离心率为( )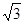
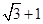
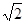
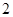
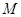 到点
到点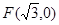 的距离与到直线
的距离与到直线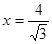 的距离之比为定值
的距离之比为定值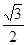 ,记
,记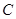 .
.
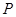 是圆
是圆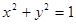 上第一象限内的任意一点,过
上第一象限内的任意一点,过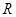 ,
,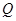 两点.
两点.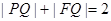 ;
;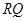 的最大值.
的最大值. ,曲线
,曲线 .自曲线
.自曲线 上一点
上一点 作
作 的两条切线切点分别为
的两条切线切点分别为 .
.
 ,求
,求 ;
; 的最大值.
的最大值.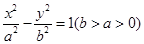 ,过右焦点
,过右焦点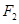 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线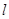 ,垂足为
,垂足为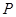 ,交另一条渐近线于
,交另一条渐近线于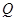 点,若
点,若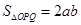 (其中
(其中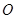 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )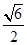
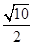
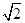
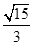
 (p>0)的准线与圆
(p>0)的准线与圆 相切,则p的值为( )
相切,则p的值为( )

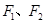 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为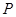 ,
,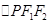 是以
是以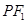 为底边的等腰三角形,若
为底边的等腰三角形,若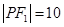 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为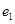 ,
,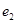 ,则
,则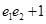 的取值范围是( )
的取值范围是( )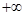 )
)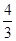 ,
,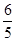 ,
,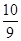 ,+
,+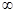 )
)