题目内容
已知双曲线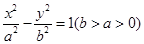 ,过右焦点
,过右焦点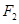 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线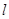 ,垂足为
,垂足为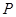 ,交另一条渐近线于
,交另一条渐近线于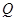 点,若
点,若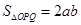 (其中
(其中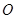 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )
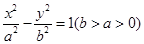 ,过右焦点
,过右焦点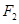 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线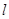 ,垂足为
,垂足为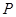 ,交另一条渐近线于
,交另一条渐近线于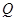 点,若
点,若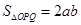 (其中
(其中 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )A.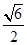 | B.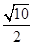 | C.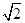 | D.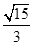 |
B
试题分析:由题意l的方程为ax+by-ac=0,则O点到直线的距离
 ,∵
,∵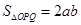 ,∴
,∴ ,又在
,又在 中,
中, ,设点Q的坐标为(m,n),则在
,设点Q的坐标为(m,n),则在 中,利用面积相等得
中,利用面积相等得 ,∴
,∴ ,联立方程
,联立方程 消x得Q的纵坐标
消x得Q的纵坐标 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,故选B
,故选B点评:解决此类问题的关键是利用题目条件找到关于a、b、c的等式关系,然后利用双曲线离心率的定义求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
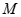 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,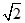 ),(0,
),(0,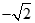 ),又点
),又点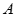
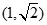 在椭圆
在椭圆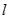 的斜率为
的斜率为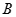 、
、 两点,求
两点,求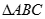 面积的最大值.
面积的最大值.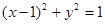 的切线(P点不在y轴上).
的切线(P点不在y轴上).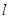 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使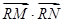 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。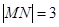 。椭圆D:
。椭圆D: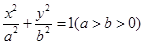 的焦距等于
的焦距等于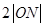 ,且过点
,且过点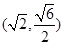
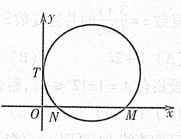
 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线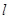 斜率的范围。
斜率的范围。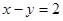 与抛物线
与抛物线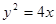 交于
交于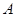 、
、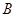 两点,则线段
两点,则线段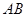 的中点坐标是 。
的中点坐标是 。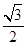 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点 的最长距离为
的最长距离为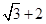 .
.
 ,若点
,若点 在
在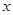 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点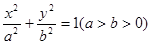 与
与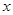 轴负半轴交于点
轴负半轴交于点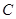 ,
,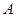 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线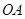 交椭圆于另一点
交椭圆于另一点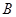 ,椭圆左焦点为
,椭圆左焦点为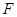 ,连接
,连接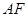 交
交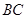 于点D。
于点D。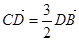 ,求椭圆的离心率;
,求椭圆的离心率; 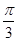 且△ABC的面积为
且△ABC的面积为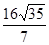 ,求椭圆的标准方程。
,求椭圆的标准方程。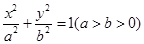 的离心率为
的离心率为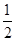 ,右焦点到直线
,右焦点到直线
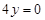 的距离为
的距离为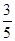 .
.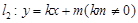 与椭圆C交于A、B两点,且线段AB中点恰好在直线
与椭圆C交于A、B两点,且线段AB中点恰好在直线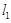 上,求△OAB的面积S的最大值.(其中O为坐标原点).
上,求△OAB的面积S的最大值.(其中O为坐标原点).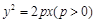 的焦点为
的焦点为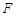 ,过焦点
,过焦点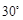 的直线交抛物线于
的直线交抛物线于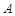 ,
,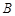 两点,点
两点,点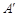 ,
,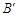 ,若四边形
,若四边形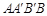 的面积为
的面积为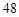 ,则抛物线的方程为____
,则抛物线的方程为____