题目内容
2.用数字0、2、3、4、6按下列要求组数、计算:(1)能组成多少个没有重复数字的三位数?
(2)可以组成多少个可以被3整除的没有重复数字的三位数?
(3)求2×3×4×6即144的所有正约数的和.(注:每小题结果都写成数据形式)
分析 (1)根据题意,分2步进行分析:①、对于百位,百位数字只能是2、3、4、6中之一,②、百位数字确定后,在剩下的4个数字中选取2个,排在十位和个位,计算出每一步的情况数目,由分步计数原理计算可得答案;
(2)由题意,能被3整除的且没有重复数字的三位数只能是由2、4、0或2、4、3或2、4、6或0、3、6组成,据此分4种情况讨论,求出每一步的选法数目,由分类计数原理计算可得答案;
(3)根据题意,分析可得144=24×32,进而由约数和公式计算可得答案.
解答 解:(1)根据题意,分2步进行分析:
①、对于百位,百位数字只能是2、3、4、6中之一,有C41种选法,
②、百位数字确定后,在剩下的4个数字中选取2个,排在十位和个位,则十位和个位数字的组成共有$A_4^2$种方法,
故可以组成没有重复数字的三位数共有${N_1}=C_4^1A_4^2=48$个;
(2)由题意,能被3整除的且没有重复数字的三位数只能是由2、4、0或2、4、3或2、4、6或0、3、6组成.
分4种情况讨论:
①、三位数由2、4、0组成,首位数字有2、4两种情况,在剩下的3个数字中选取2个,排在十位和个位,此时共有C21A22种选法;
②、三位数由2、4、3组成,将3个数字全排列,排在百位、十位和个位,此时有A33种选法;
③、三位数由2、4、6组成,将3个数字全排列,排在百位、十位和个位,此时有A33种选法;
④、三位数由0、3、6组成,首位数字有3、6两种情况,在剩下的3个数字中选取2个,排在十位和个位,此时共有C21A22种选法;
共有${N_2}=C_2^1A_2^2+2A_3^3+C_2^1A_2^2=20$个被3整除的没有重复数字的三位数,
(3)根据题意,144=24×32,
则144的所有正约数的和为${N_3}=(1+2+{2^2}+{2^3}+{2^4})(1+3+{3^2})=403$.
点评 本题考查排列、组合的应用,涉及分步计数原理、分类计数原理的应用,(3)的关键是正确运用约数和公式.

| A. | 若a=0,则y=f(x)与y=3是同一函数 | |
| B. | 若0<a≤1,则$f(-\frac{π}{2})<f(2-{log_3}2)<f[{(\frac{1}{3})^{{{log}_3}\frac{2}{3}}}]<f({log_3}5)<f(\frac{π}{2})$ | |
| C. | 若a=2,则对任意使得f(m)=0的实数m,都有f(-m)=1 | |
| D. | 若a>3,则f(cos2)<f(cos3) |
| A. | 存在满足x<y的x,y∈[a,b]使得f(x)>f(y) | |
| B. | 不存在x,y∈[a,b]满足x<y且f(x)≤f(y) | |
| C. | 对任意满足x<y的x,y∈[a,b]都有f(x)>f(y) | |
| D. | 存在满足x<y的x,y∈[a,b]都有f(x)≤f(y) |
| A. | (0,1) | B. | [0,1] | C. | (-1,0) | D. | [-1,0] |
| A. | (0,$\frac{1}{32}$) | B. | ($\frac{1}{32}$,0) | C. | (2,0) | D. | (0,2) |
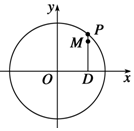 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.