题目内容
已知椭圆的中心为原点O,长轴在x轴上,短半轴长为
,离心率e=
,左、右焦点分别为F1、F2.
(Ⅰ)求该椭圆的方程;
(Ⅱ)过F1作直线l交椭圆于P、Q两点(直线l不过原点O),若
•
=
,求直线l的方程.
| ||
| 2 |
| ||
| 5 |
(Ⅰ)求该椭圆的方程;
(Ⅱ)过F1作直线l交椭圆于P、Q两点(直线l不过原点O),若
| QF2 |
| PF2 |
| 11 |
| 8 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意知
,由此能求出椭圆的方程.
(Ⅱ)设直线l的方程为:x=my-1,设P(x1,y1),Q(x2,y2),由
,得(6m2+10)y2-12my-9=0,由此利用韦达定理结合已知条件能求出直线l的方程.
|
(Ⅱ)设直线l的方程为:x=my-1,设P(x1,y1),Q(x2,y2),由
|
解答:
解:(Ⅰ)设所求椭圆的标准方程为
+
=1(a>b>0),
短半轴长为
,离心率e=
,
则
,…(3分)
解得:a2=
,b2=
,c2=1,
因此所求椭圆的方程为:
+
=1.…(6分)
(Ⅱ)由(Ⅰ)知F1(-1,0)、F2(1,0),
由题意知直线(x0-a)2+(
-
)2=a2+
的倾斜角不为0,
故可设直线l的方程为:x=my-1,…(7分)
设P(x1,y1),Q(x2,y2),
由
,整理得(6m2+10)y2-12my-9=0,
△>0,y1+y2=
,y1•y2=-
①,…(8分)
又
=(1-x1,-y1),
=(1-x2,-y2),
所以
=(11-x)•(1-x2)+y1y2
=(2-my1)•(2-my2)+y1y2
=(m2+1)y1y2-2m(y1+y2)+4=
,
由
•
=
,解得m=±1,…(10分)
所以满足条件的直线有两条,其方程分别为:x+y+1=0和x-y+1=0.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
短半轴长为
| ||
| 2 |
| ||
| 5 |
则
|
解得:a2=
| 5 |
| 2 |
| 3 |
| 2 |
因此所求椭圆的方程为:
| 2x2 |
| 5 |
| 2y2 |
| 3 |
(Ⅱ)由(Ⅰ)知F1(-1,0)、F2(1,0),
由题意知直线(x0-a)2+(
| x02 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
故可设直线l的方程为:x=my-1,…(7分)
设P(x1,y1),Q(x2,y2),
由
|
△>0,y1+y2=
| 12m |
| 6m2+10 |
| 9 |
| 6m2+10 |
又
| PF2 |
| QF2 |
所以
| PF2• |
| QF2 |
=(2-my1)•(2-my2)+y1y2
=(m2+1)y1y2-2m(y1+y2)+4=
| -9m2+31 |
| 6m2+10 |
由
| QF2 |
| PF2 |
| 11 |
| 8 |
所以满足条件的直线有两条,其方程分别为:x+y+1=0和x-y+1=0.…(12分)
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
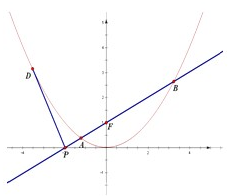 抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.
抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.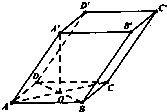 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=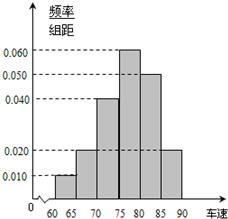 某调查公司在某服务区调查七座以下小型汽车在某段高速公路的车速(km/t),办法是按汽车进服务区的先后每间隔50辆抽取一辆的抽样方法抽取40名驾驶员进行询问,将调查结果按[60,65)[65,70)[70,75)[75,80),[80,85)[85,90)分成六段,并得到如图所示的频率分布直方图.
某调查公司在某服务区调查七座以下小型汽车在某段高速公路的车速(km/t),办法是按汽车进服务区的先后每间隔50辆抽取一辆的抽样方法抽取40名驾驶员进行询问,将调查结果按[60,65)[65,70)[70,75)[75,80),[80,85)[85,90)分成六段,并得到如图所示的频率分布直方图.