题目内容
 如图,由抛物线C1:y2=4x与C2:y2=8(3-x)围成一个封闭图形OACB,F是抛物线的焦点,直线y=h(h<2)交两弧于P、Q两点,则当h=
如图,由抛物线C1:y2=4x与C2:y2=8(3-x)围成一个封闭图形OACB,F是抛物线的焦点,直线y=h(h<2)交两弧于P、Q两点,则当h=考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:利用直线的方程两个抛物线的方程求出点的坐标,在求出距离,把h|PQ|转化关于h的式子,最后利用导数解决问题
解答:
解:抛物线C1:y2=4x与C2:y2=8(3-x),直线y=h(h<2)
∵抛物线C1和C2都与直线y=h(h<2)相交,且交点为p,Q
∴P(
,h),Q(3-
,h)
|PQ|=3-
即h|PQ|=3h-
设f(h)=3h-
h<2
可得f(h)′=3-
h<2,令3-
=0得h=
由f(h)′>0,h<
;f(h)′<0
<h<2
所以f(h)=3h-
h<2,在区间(-∞,
)上单调递增,在区间(
,2)上单调递减
故当h=
h|PQ|最大
∵抛物线C1和C2都与直线y=h(h<2)相交,且交点为p,Q
∴P(
| h2 |
| 4 |
| h2 |
| 8 |
|PQ|=3-
| 3h2 |
| 8 |
| 3h3 |
| 8 |
设f(h)=3h-
| 3h3 |
| 8 |
可得f(h)′=3-
| 9h2 |
| 8 |
| 9h2 |
| 8 |
2
| ||
| 3 |
由f(h)′>0,h<
2
| ||
| 3 |
2
| ||
| 3 |
所以f(h)=3h-
| 3h3 |
| 8 |
2
| ||
| 3 |
2
| ||
| 3 |
故当h=
2
| ||
| 3 |
点评:本题考察了用函数的思想解决圆锥曲线的最值问题,因为是三次函数必需借助导数才能解决

练习册系列答案
相关题目
函数f(x)=2sin(x-
),x∈[-π,0]的单调递增区间是( )
| π |
| 3 |
A、[-π,-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
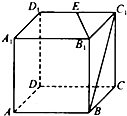 如图,在正方体ABCD-A1B1C1D1中,棱长AB=2,点E是棱C1D1的中点,则异面直线B1E和BC1所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,棱长AB=2,点E是棱C1D1的中点,则异面直线B1E和BC1所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|