题目内容
5.已知$sin(π-α)=\frac{3}{5}$,且$α∈(0,\frac{π}{2})$,那么tanα=$\frac{3}{4}$.分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵已知$sin(π-α)=\frac{3}{5}$=sinα,且$α∈(0,\frac{π}{2})$,∴cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{4}{5}$,
那么tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
18.设P点为角α的终边与单位圆O的交点,且sinα=MP,cosα=OM,则下列命题成立的是( )
| A. | 总有MP+OM>1 | B. | 总有MP+OM=1 | ||
| C. | 存在角α,使MP+OM=1 | D. | 不存在角α,使MP+OM<0 |
20.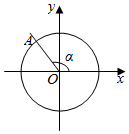 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
17.从点P(-2,1)向圆x2+y2-2x-2my+m2=0作切线,当切线长最短时,m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
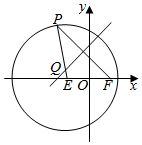 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.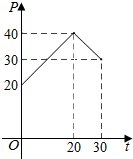 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.