题目内容
2.已知实数x,y满足不等式组$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0\end{array}\right.$,则x2+y2的取值范围是[1,25].分析 作出不等式组$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0\end{array}\right.$对应的平面区域,利用x2+y2的几何意义求最值.
解答 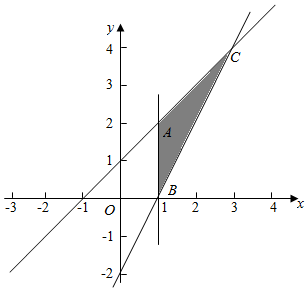 解:设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.
解:设z=x2+y2,则z的几何意义为动点P(x,y)到原点距离的平方.
作出不等式组$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0\end{array}\right.$对应的平面区域如图:
由$\left\{\begin{array}{l}{x-y+1=0}\\{2x-y-2=0}\end{array}\right.$得C(3,4),由图象可知点C(3,4)到原点的距离最大,最大值为5.
点B(1,0)到原点的距离最小,最小值为z=1.
x2+y2的取值范围是[1,25].
故答案为:[1,25].
点评 本题主要考查两点间的距离公式,以及简单线性规划的应用,利用目标函数的几何意义是解决线性规划内容的基本方法,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
10.i是虚数单位,复数$\frac{3+4i}{1-2i}$=( )
| A. | 1+2i | B. | 1-2i | C. | -1+2i | D. | -1-2i |
7.在${(x-\frac{1}{2x})^6}$的展开式中,x4的系数为( )
| A. | -3 | B. | $-\frac{1}{2}$ | C. | 3 | D. | 6 |
11.已知函数fM(x)的定义域为实数集R,满足狄利克雷函数fM(x)=$\left\{\begin{array}{l}1,x∈M\\ 0,x∉M\end{array}$(M是R的非空真子集),在R上有两个非空真子集A,B,且A∩B=∅,则F(x)=$\frac{{{f_{A∪B}}(x)+1}}{{{f_A}(x)+{f_B}(x)+1}}$的值域为( )
| A. | (0,$\frac{2}{3}$] | B. | {1} | C. | {$\frac{1}{2}$,$\frac{2}{3}$,1} | D. | [$\frac{1}{3}$,1] |
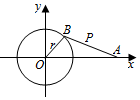 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.