题目内容
11.P是棱长为2的正四面体内任意一点,则它到该正四面体各个面的距离之和等于$\frac{2\sqrt{6}}{3}$.分析 先求出正四面体的体积,利用正四面体的体积相等,求出它到四个面的距离.
解答 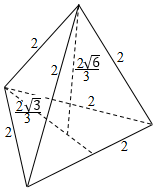 解:因为正四面体的体积等于四个三棱锥的体积和,
解:因为正四面体的体积等于四个三棱锥的体积和,
设它到四个面的距离分别为a,b,c,d,
由于棱长为1的正四面体,故四个面的面积都是 $\frac{1}{2}$×2×2×sin60°=$\sqrt{3}$.
又顶点到底面的投影在底面的中心,此点到底面三个顶点的距离都是高的
,又高为2×sin60°=$\sqrt{3}$,
故底面中心到底面顶点的距离都是:$\frac{2\sqrt{3}}{3}$.
由此知顶点到底面的距离是 $\sqrt{{2}^{2}-({\frac{2\sqrt{3}}{3})}^{2}}$=$\frac{2\sqrt{6}}{3}$.
此正四面体的体积是 $\frac{1}{3}$×$\sqrt{3}$×$\frac{2\sqrt{6}}{3}$=$\frac{1}{3}$×$\sqrt{3}$×(a+b+c+d).
所以:a+b+c+d=$\frac{2\sqrt{6}}{3}$.
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题是中档题,考查正四面体的体积的计算,转化思想的应用,考查空间想象能力,计算能力.

练习册系列答案
相关题目
1.在复平面内,复数z=$\frac{2}{1-i}$-2i3(i为虚数单位)表示的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.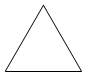 一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )
一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )
 一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )
一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )| A. | 8 | B. | $8\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
16.下面几种推理过程是演绎推理的是( )
| A. | 某校高三有8个班,1班有51人,2班有53人,由此推断各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 在数列{an}中,a1=1,an+1=$\frac{{a}_{n}}{1+{a}_{n}}$(n=1,2,3),由此归纳出{an}的通项公式 | |
| D. | 三角函数都是周期函数,tanα是三角函数,因此tanα是周期函数 |