题目内容
6.在如下程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{4}$ |
分析 根据查询框图转化为几何概型进行计算即可.
解答 解:程序框图对应的不等式组为$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$,
则“恭喜中奖!满足条件为y≥x+$\frac{1}{2}$,
作出不等式组对应的平面区域如图: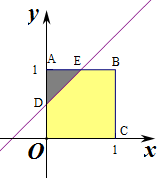
则正方形的面积S=1×1=1,
D(0,$\frac{1}{2}$),E($\frac{1}{2}$,1),
则△ADE的面积S=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{8}$,
则能输出“恭喜中奖!”的概率为$\frac{1}{8}$,
故选:A
点评 本题主要考查几何概型的概率的计算,根据程序框图转化为几何概型是解决本题的关键.

练习册系列答案
相关题目
7.某小区停车场的收费标准为:每车每次停车时间不超过2小时免费,超过2小时的部分每小时收费1元(不足1小时的部分按1小时计算).现有甲乙两人独立来停车场停车(各停车一次),且两人停车时间均不超过5小时.设甲、乙两人停车时间(小时)与取车概率如表所示.
(1)求甲、乙两人所付车费相同的概率;
(2)设甲、乙两人所付停车费之和为随机变量ξ,求ξ的分布列和数学期望Eξ.
 | (0,2] | (2,3] | (3,4] | (4,5] |
| 甲 | $\frac{1}{2}$ | x | x | x |
| 乙 | $\frac{1}{6}$ | $\frac{1}{3}$ | y | 0 |
(2)设甲、乙两人所付停车费之和为随机变量ξ,求ξ的分布列和数学期望Eξ.
17.在△ABC中,若BC=2,A=60°,则$\overrightarrow{AB}$•$\overrightarrow{CA}$有( )
| A. | 最大值-2 | B. | 最小值-2 | C. | 最大值2$\sqrt{3}$ | D. | 最小值2$\sqrt{3}$ |
11.若点P为椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的动点,G点满足$\overrightarrow{PG}$=2$\overrightarrow{GO}$(O是坐标原点),则G的轨迹方程为( )
| A. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 | B. | $\frac{4{x}^{2}}{9}$+y2=1 | C. | $\frac{9{x}^{2}}{4}$+3y2=1 | D. | x2+$\frac{4{y}^{2}}{3}$=1 |
18.已知p1:直线l1:x-y-1=0与直线l2:x+ay-2=0平行,q:a=-1,则p是q的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |