题目内容
11.若点P为椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的动点,G点满足$\overrightarrow{PG}$=2$\overrightarrow{GO}$(O是坐标原点),则G的轨迹方程为( )| A. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 | B. | $\frac{4{x}^{2}}{9}$+y2=1 | C. | $\frac{9{x}^{2}}{4}$+3y2=1 | D. | x2+$\frac{4{y}^{2}}{3}$=1 |
分析 设P(x0,y0),G(x,y),则$\overrightarrow{PG}$=(x-x0,y-y0),$\overrightarrow{GO}$=(-x,-y),由$\overrightarrow{PG}$=2$\overrightarrow{GO}$,即可求得$\left\{\begin{array}{l}{{x}_{0}=3x}\\{{y}_{0}=3y}\end{array}\right.$,代入椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,即可求得G的轨迹方程.
解答 解:设P(x0,y0),G(x,y),由$\overrightarrow{PG}$=(x-x0,y-y0),$\overrightarrow{GO}$=(-x,-y),
由$\overrightarrow{PG}$=2$\overrightarrow{GO}$,即$\left\{\begin{array}{l}{x-{x}_{0}=-2x}\\{y-{y}_{0}=-2y}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{{x}_{0}=3x}\\{{y}_{0}=3y}\end{array}\right.$,
由P在椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,则$\frac{9{x}^{2}}{4}+3{y}^{2}=1$,
故选C.
点评 本题考查椭圆的标准方程,考查向量与圆锥曲线的应用,考查轨迹方程的求法,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.函数y=sin(2x+φ)的图象向右平移$\frac{π}{3}$个单位,与函数y=sin2x的图象重合,φ∈(-π,π),则φ=( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | -$\frac{5π}{6}$ | D. | $\frac{π}{3}$ |
19.近几年,“互联网+”已经影响了多个行业,在线教育作为现代信息技术同教育相结合的产物,也引发了教育领域的变革.目前在线教育主要包括在线测评、在线课堂、自主学习、线下延伸四种模式.为了解学生参与在线教育情况,某区从2000名高一学生中随机抽取了200名学生,对他们参与的在线教育模式进行调查,其调查结果整理如下:(其中标记“√”表示参与了该项在线教育模式).
(Ⅰ)试估计该区高一学生中参与在线课堂教育模式的人数;
(Ⅱ)在样本中用分层抽样的方法从参与自主学习的学生中抽取5人,现从这5人中随机抽取2人,求这2人都参与线下延伸教育模式的概率.
教育模式 人数(人) | 在线测评 | 在线课堂 | 自主学习 | 线下延伸 |
| 25 | √ | √ | √ | |
| 45 | √ | |||
| 40 | √ | √ | ||
| 30 | √ | √ | √ | |
| 40 | √ | √ | ||
| 20 | √ | √ |
(Ⅱ)在样本中用分层抽样的方法从参与自主学习的学生中抽取5人,现从这5人中随机抽取2人,求这2人都参与线下延伸教育模式的概率.
6.在如下程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )

| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{4}$ |
16.设$f(x)=\frac{x}{{\sqrt{1+{x^2}}}}$,数列{an}满足a1=f(1),an+1=f(an)(n∈N*),则a2017=( )
| A. | $\frac{1}{{\sqrt{2016}}}$ | B. | $\frac{1}{{\sqrt{2017}}}$ | C. | $\frac{1}{{\sqrt{2018}}}$ | D. | $\frac{1}{{\sqrt{2019}}}$ |
3.已知全集N=Z,集合A={-1,1,2,3,4},B={-2,-1,0,1,2},则(∁UA)∩B=( )
| A. | {3,4} | B. | {-2,3} | C. | {-2,4} | D. | {-2,0} |
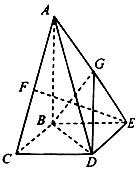 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE=$\sqrt{2}$.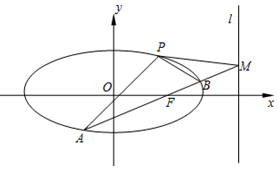 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.