题目内容
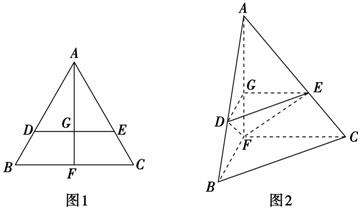
如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=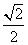 .
.
(1)证明:DE//平面BCF;(2)证明:CF⊥平面ABF;
(3)当AD=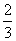 时,求三棱锥F-DEG的体积VF-DEG.
时,求三棱锥F-DEG的体积VF-DEG.
(1)证明:在等边三角形ABC中,AD=AE.
∴ =
= ,在折叠后的三棱锥ABCF中也成立,
,在折叠后的三棱锥ABCF中也成立,
∴DE∥BC,∵DE⊄平面BCF,
BC⊂平面BCF,∴DE∥平面BCF.
(2)证明:在等边三角形ABC中,F是BC的中点,所以AF⊥BC,①
BF=CF= .
.
∵在三棱锥A-BCF中,BC=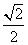 ,∴BC2=BF2+CF2,
,∴BC2=BF2+CF2,
∴CF⊥BF,②
∵BF∩CF=F,∴CF⊥平面ABF.
(3)解析:由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.
∴VF-DEG=VE-DFG= ×
× ·DG·FG·GE=
·DG·FG·GE= ×
× ×
× ×
× ×
× =
= .
.

练习册系列答案
相关题目

 体的
体的 正视图和俯视图.(1)试判断该几何体是什
正视图和俯视图.(1)试判断该几何体是什 ,并求该平面图形的面积;(3)求出该几何
,并求该平面图形的面积;(3)求出该几何
 序号是( )
序号是( )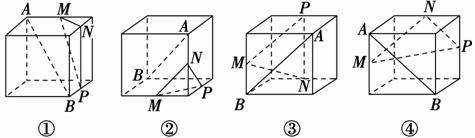
 C.②③ D.②④
C.②③ D.②④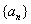 的前
的前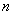 项和为
项和为 ,满足
,满足 .
.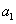 的值;
的值;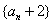 是等比数列,并求数列
是等比数列,并求数列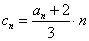 ,求数列
,求数列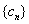 的前
的前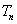
 的图象向左平移
的图象向左平移 个单位,若所得的图象与原图象重合,则
个单位,若所得的图象与原图象重合,则 的值不可能等于( )
的值不可能等于( ) C.8 D.12
C.8 D.12