题目内容
19.若(1+a)n(a>0)的展开式中所有项系数和为64,且展开式的第三项等于15,则a的值为1.分析 根据展开式中所有项系数和求出n的值,再根据展开式的第三项求出a的值.
解答 解:∵(1+a)n(a>0)的展开式中所有项系数和为64,
∴(1+1)n=64,
解得n=6;
又展开式的第三项为T3=${C}_{6}^{2}$•a2=15,
解得a=±1,又a>0,
故答案为:1.
点评 本题考查了二项式展开式定理的应用问题,也考查了展开式的通项公式应用问题,是基础题目.

练习册系列答案
相关题目
7.下列四个图形中,不是以x为自变量的函数的图象是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知在空间坐标系O-xyz中,点A(-1,2,3)关于平面xOz对称的点的坐标为( )
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (-1,-2,-3) |
9.已知函数f(x)=mx-m2-4,(m>0,x∈R).若a2+b2=8,则$\frac{f(b)}{f(a)}$的取值范围是( )
| A. | [$\sqrt{3}$-2,$\sqrt{3}$+2] | B. | [2-$\sqrt{3}$,2+$\sqrt{3}$] | C. | [0,2+$\sqrt{3}$] | D. | [0,2-$\sqrt{3}$] |
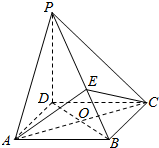 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.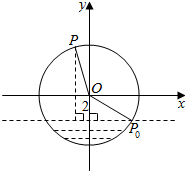 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.