题目内容
已知函数f(x)=ax2-bx+1的零点为-
,
,则a为 .b为 .
| 1 |
| 2 |
| 1 |
| 3 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:把函数的零点转化为方程的根,然后利用根与系数的关系列式求得a,b的值.
解答:
解:∵函数f(x)=ax2-bx+1的零点为-
,
,
∴-
,
是方程ax2-bx+1=0的两个根,
则
,解得:a=-6,b=1.
故答案为:-6;1.
| 1 |
| 2 |
| 1 |
| 3 |
∴-
| 1 |
| 2 |
| 1 |
| 3 |
则
|
故答案为:-6;1.
点评:本题考查了函数的零点与方程根的关系,考查了根与系数的关系的应用,是基础题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
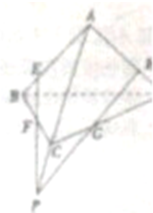

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |
 如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若
如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若 如图,椭圆E:
如图,椭圆E: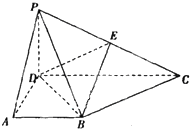 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.