题目内容
14.已知A为锐角△ABC的内角,且 sinA-2cosA=a(a∈R).(Ⅰ)若a=-1,求tanA的值;
(Ⅱ)若a<0,且函数f(x)=(sinA)•x2-(2cosA)•x+1在区间[1,2]上是增函数,求sin2A-sinA•cosA的取值范围.
分析 (Ⅰ)利用同角三角函数的基本关系,求得sinA和cosA的值,可得tanA的值.
(2)由题意可得1≤tanA<2,化简要求式子为-$\frac{1}{t+\frac{2}{t}-2}$,再利用函数的单调性求得它的范围.
解答 解:(Ⅰ)锐角△ABC中,a=-1,由题意可得$\left\{{\begin{array}{l}{sinA-2cosA=-1}\\{{{sin}^2}A+{{cos}^2}A=1}\end{array}}\right.$,
求得$\left\{{\begin{array}{l}{cosA=\frac{4}{5}}\\{sinA=\frac{3}{5}}\end{array}}\right.$,或$\left\{{\begin{array}{l}{cosA=0}\\{sinA=1}\end{array}}\right.$(舍去),∴$tanA=\frac{3}{4}$.
(Ⅱ)若a<0,由题意可得sinA-2cosA<0,得tanA<2,又$\frac{cosA}{sinA}≤1$,tanA≥1,
∴1≤tanA<2,∴${sin^2}A-sinA•cosA=\frac{{{{sin}^2}A-sinA•cosA}}{{{{sin}^2}A+{{cos}^2}A}}=\frac{{{{tan}^2}A-tanA}}{{{{tan}^2}A+1}}$=$-\frac{1+tanA}{{{{tan}^2}A+1}}+1$,
令t=tanA+1,2≤t<3,∴${sin^2}A-sinA•cosA=-\frac{t}{{{t^2}-2t+2}}+1=-\frac{1}{{t+\frac{2}{t}-2}}+1$,
∵y=$t+\frac{2}{t}-2$在[2,3)上递增,∴$1≤t+\frac{2}{t}-2<\frac{5}{3}$,∴$0≤-\frac{1}{{t+\frac{2}{t}-2}}+1<\frac{2}{5}$.
即sin2A-sinA•cosA的取值范围为$[0,\frac{2}{5})$.
点评 本题主要考查同角三角函数的基本关系,利用函数的单调性求函数的值域,属于中档题.

| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
| A. | -4 | B. | 4 | C. | -1 | D. | 1 |
| A. | (1,3] | B. | [1,3] | C. | [-1,3] | D. | (-1,3] |
| A. | 3 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $3+\sqrt{2}$ |
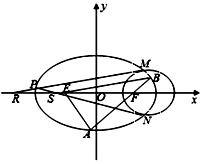 已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$
已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$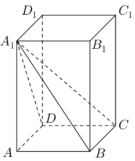 如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;
如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3; 如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.
如图所示,抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率存在的直线l交抛物线C于A,B两点,已知当直线l的斜率为1时,|AB|=8.