题目内容
5.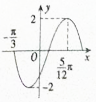 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
分析 利用函数的图象确定周期T的值,利用周期公式确定ω,再根据图象过点($\frac{5π}{12}$,2),确定φ的值,即可求函数f(x)的解析式,由函数y=Asin(ωx+φ)的图象变换可得结论.
解答 解:由图象可得,$\frac{3T}{4}$=$\frac{5π}{12}$-(-$\frac{π}{3}$),解得T=π,
由T=$\frac{2π}{ω}$=π,得ω=2.
因为图象过点($\frac{5π}{12}$,2),
所以2sin(2×$\frac{5π}{12}$+φ)=2,
则$\frac{5π}{6}$+φ=2kπ+$\frac{π}{2}$,得φ=2kπ-$\frac{π}{3}$,k∈Z,
由-$\frac{π}{2}$<φ<$\frac{π}{2}$,得φ=-$\frac{π}{3}$,
f(x)=2sin(2x-$\frac{π}{3}$),
所以将g(x)=2sin2x的图象向右平移$\frac{π}{6}$个单位得到函数f(x)=2sin(2x-$\frac{π}{3}$).
故答案为:$\frac{π}{6}$.
点评 本题考查三角函数解析式的确定,考查图象的变换,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
13.棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,则线段D1E的长度为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知集合A=$\{x|y=\sqrt{x-1}\}$,A∩B=ϕ,则集合B不可能是( )
| A. | {x|x<-1} | B. | {(x,y)|y=x-1} | C. | {y|y=-x2} | D. | {x|x≥-1} |
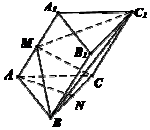 如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.
如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.