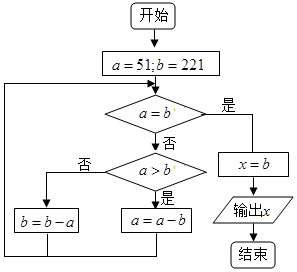
题目内容
13.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+3≥0}\\{2x+y-4≤0}\\{y+a≥0}\end{array}\right.$,若z=y-2x的最大值为7,则实数a=( )| A. | -1 | B. | 1 | C. | $\frac{10}{3}$ | D. | $\frac{11}{2}$ |
分析 根据已知的约束条件 画出满足约束条件的可行域,再用目标函数的几何意义,通过目标函数的最值,得到最优解,代入方程即可求解a值.
解答 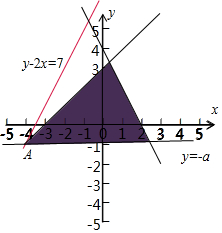 解:作出不等式组$\left\{\begin{array}{l}{x-y+3≥0}\\{2x+y-4≤0}\\{y+a≥0}\end{array}\right.$表示的平面区域,如图所示:
解:作出不等式组$\left\{\begin{array}{l}{x-y+3≥0}\\{2x+y-4≤0}\\{y+a≥0}\end{array}\right.$表示的平面区域,如图所示:
令z=y-2x,则z表示直线z=y-2x在y轴上的截距,截距越大,z越大,
结合图象可知,当z=y-2x经过点A时z最大,
由$\left\{\begin{array}{l}{y-2x=7}\\{x-y+3=0}\end{array}\right.$可知A(-4,-1),
A(-4,-1)在直线y+a=0上,可得a=1.
故选:B.
点评 本题考查的知识点是线性规划,考查画不等式组表示的可行域,考查数形结合求目标函数的最值.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,若这个几何体的顶点都在球O的表面上,则球O的表面积是( )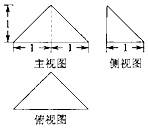

| A. | 2π | B. | 4π | C. | 5π | D. | 20π |
4.已知集合A={x|x2-5x-6≤0},$B=\left\{{\left.x\right|\frac{1}{x-1}>0}\right\}$,则A∩B等于( )
| A. | [-1,6] | B. | (1,6] | C. | [-1,+∞) | D. | [2,3] |