题目内容
18.已知等差数列{an},等比数列{bn}的前n项和为Sn,Tn(n∈N*),若Sn=$\frac{3}{2}$n2+$\frac{1}{2}$n,b1=a1,b2=a3,则an=3n-1,Tn=$\frac{2}{3}({4}^{n}-1)$.分析 利用a1=2=b1,n≥2时,an=Sn-Sn-1,可得an.b2=a3=8,公比q=4.再利用等比数列的求和公式即可得出.
解答 解:a1=2=b1,
n≥2时,an=Sn-Sn-1=$\frac{3}{2}$n2+$\frac{1}{2}$n-$[\frac{3}{2}(n-1)^{2}+\frac{1}{2}(n-1)]$=3n-1.
n=1时也成立,∴an=3n-1.
b2=a3=8,公比q=$\frac{8}{2}$=4.
∴Tn=$\frac{2({4}^{n}-1)}{4-1}$=$\frac{2}{3}({4}^{n}-1)$.
故答案为:3n-1,$\frac{2}{3}({4}^{n}-1)$.
点评 本题主要考查了数列递推关系、等比数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知复数z满足(1+i)z=1+3i(i是虚数单位),则z的共轭复数为( )
| A. | 1-i | B. | 1+i | C. | 2-i | D. | 2+i |
9.抛物线y2=4x的焦点为F,点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )
| A. | 4 | B. | 5 | C. | $4+2\sqrt{2}$ | D. | $5+\sqrt{5}$ |
6.已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
13.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+3≥0}\\{2x+y-4≤0}\\{y+a≥0}\end{array}\right.$,若z=y-2x的最大值为7,则实数a=( )
| A. | -1 | B. | 1 | C. | $\frac{10}{3}$ | D. | $\frac{11}{2}$ |
10.设集合P={1,2,3,4},Q={x||x|≤3,x∈R},则P∩Q等于( )
| A. | {1} | B. | {1,2,3} | ||
| C. | {3,4} | D. | {-3,-2,-1,0,1,2,3} |
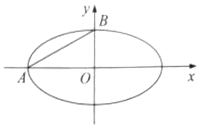 已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.
已知点A(-2,0),B(0,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上.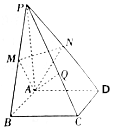 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.