题目内容
15.边长为4$\sqrt{3}$的等边△ABC中,D为边AB的中点,若P为线段CD的中点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的值为( )| A. | 18 | B. | -18 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
分析 可画出图形,根据条件即可求出CD=6,并且根据向量加法平行四边形法则及相反向量概念即可得到$\overrightarrow{PA}+\overrightarrow{PB}=-2\overrightarrow{PC}$,从而带入$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$进行向量数量积的运算即可求出该值的大小.
解答 解:如图,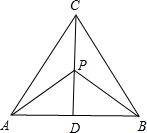
根据条件,CD=$4\sqrt{3}×\frac{\sqrt{3}}{2}$=6,CP=3,
$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PD}=-2\overrightarrow{PC}$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}=-2{\overrightarrow{PC}}^{2}=-18$.
故选B.
点评 考查等边三角形的中线也是高线,三角函数定义,以及向量加法的平行四边形法则,向量的数乘运算,向量数量积的计算公式.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
6.已知集合A={x|x2-x-2<0},B=$\{x|y=lg\frac{1-x}{1+x}\}$,在区间(-3,3)上任取一实数x,则x∈A∩B的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
7.若抛物线y2=-16x上一点P到x轴的距离为12,则该点到焦点的距离为( )
| A. | 5 | B. | 8 | C. | -5 | D. | 13 |
5.抛掷一枚骰子,向上的面的点数是5或6的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 1 |
 如图所示,有一圆锥形容器,其底面半径等于圆锥的高,若以72πcm3/s的速度向该容器注水,则水深10cm时水面上升的速度为$\frac{18}{25}$cm/s.
如图所示,有一圆锥形容器,其底面半径等于圆锥的高,若以72πcm3/s的速度向该容器注水,则水深10cm时水面上升的速度为$\frac{18}{25}$cm/s.