题目内容
某家具厂根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产A、B、C三种型号的沙发共120套,且C型号沙发至少生产20套.已知生产这些沙发每套所需工时和每套产值如表:
| 沙发型号 | A型号 | B型号 | C型号 |
| 工时 |
|
|
|
| 产值/千元 | 4 | 3 | 2 |
问每周应生产A、B、C型号的沙发各多少套,才能使产值最高?最高产值是多少?(以千元为单位)
解:设每周生产A型号沙发 套,B型号沙发
套,B型号沙发 套,则生产C型号沙发120-
套,则生产C型号沙发120- -
- 套,产值为
套,产值为 。目标函数为
。目标函数为 =
= ,
,
题目中包含的约束条件为

 ,即
,即
可行域如图所示
可得 (10,90), 所以
(10,90), 所以 (千元) 分
(千元) 分
答:每周应生产A、B、C型号的沙发分别为10套、90套、20套,才能使产值最高,最高产值是350千元。 …………12分

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若圆C1:x2+y2+2ax+a2﹣4=0,(a∈R)与圆C2:x2+y2﹣2by﹣1+b2=0,(b∈R)外切,则a+b的最大值为( )
|
| A. |
| B. | ﹣3 | C. | 3 | D. | 3 |
若关于x的一元二次不等式ax2+bx+c>0的解集是空集,则( )
|
| A. |
| B. |
| C. |
| D. |
|



 ,tanβ=
,tanβ= ,且α、β∈
,且α、β∈ .
. .
. ,那么n=_______
,那么n=_______ 


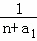 +
+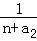 +
+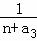 +…+
+…+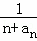 (n∈N*,且n≥2),函数f(n)的最小值 _________ .
(n∈N*,且n≥2),函数f(n)的最小值 _________ .



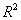 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;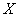 与
与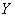 ,若它们的随机变量
,若它们的随机变量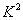 的观测值
的观测值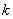 越小,则判断“
越小,则判断“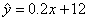 中,当解释变量
中,当解释变量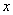 每增加一个单位时,预报变量
每增加一个单位时,预报变量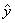 平均增加
平均增加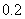 个单位。
个单位。