题目内容
若圆C1:x2+y2+2ax+a2﹣4=0,(a∈R)与圆C2:x2+y2﹣2by﹣1+b2=0,(b∈R)外切,则a+b的最大值为( )
|
| A. |
| B. | ﹣3 | C. | 3 | D. | 3 |
C

练习册系列答案
相关题目
直线l1:( ﹣1)x+y﹣2=0与直线l2:(
﹣1)x+y﹣2=0与直线l2:( +1)x﹣y﹣3=0的位置关系是( )
+1)x﹣y﹣3=0的位置关系是( )
|
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 重合 |
某家具厂根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产A、B、C三种型号的沙发共120套,且C型号沙发至少生产20套.已知生产这些沙发每套所需工时和每套产值如表:
| 沙发型号 | A型号 | B型号 | C型号 |
| 工时 |
|
|
|
| 产值/千元 | 4 | 3 | 2 |
问每周应生产A、B、C型号的沙发各多少套,才能使产值最高?最高产值是多少?(以千元为单位)


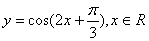 的图象,只需把函数
的图象,只需把函数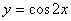 的图象 ( )
的图象 ( )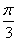 个单位长度 B. 向右平行移动
个单位长度 B. 向右平行移动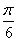 个单位长度 D. 向右平行移动
个单位长度 D. 向右平行移动
 中,
中, ,点E在
,点E在 ,且
,且 .
. ;
; 平面角的余弦值.
平面角的余弦值.
 ,其余各棱长都为2,则二面角A﹣BD﹣C的大小为 _________ .
,其余各棱长都为2,则二面角A﹣BD﹣C的大小为 _________ .


 的前n项和Sn.
的前n项和Sn.