对数函数y=log2+2014的恒过定点为．题目和参考答案——青夏教育精英家教网—

题目内容

对数函数y=log₂（x+2013）+2014的恒过定点为

．

考点：对数函数的单调性与特殊点

专题：函数的性质及应用

分析：令对数的真数等于零，求得x、y的值，可得函数y=log₂（x+2013）+2014所过定点的坐标．

解答： 解：令x+2013=1，求得x=-2012，y=2014，故函数y=log₂（x+2013）所过定点是（-2012，2014），
故答案为：（-2012，2014）．

点评：本题主要考查对数函数的单调性和特殊点，属于基础题．

练习册系列答案

相关题目

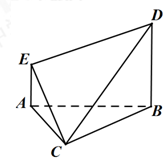如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1
（Ⅰ）求二面角C-BD-A的大小；
（Ⅱ）求直线CE与平面BCD所成角的正弦值．

设有关于x的方程ax²-2bx+a=0．
（1）若a是从1，2两个数中任取的一个数，b是从1，2，3，4，5五个数中任取的一个数，求上述方程有实根的概率；
（2）若a是从区间[1，2]任取的一个数，b是从区间[1，5]任取的一个数，求上述方程没有实根的概率．

已知数列{a_n}的各项为正数，其前n项和S_n满足S_n=(

an+1

)2，设b_n=20-a_n（n∈N^*）
（1）求证：数列{a_n}是等差数列，并求{a_n}的通项公式；
（2）求数列{|b_n|}的前n项和B_n．

求f（x）=4^x-3•2^x+2的单调区间和最小值．

已知函数f（x）=

1，x≥0

1-x2，x＜0

，则满足不等式f（1-x²）＞f（2x）的x的取值集合是

，求f（x）的单调区间，并比较f（-π）与f（

）的大小．

函数y+1=

x-1

的图象与函数y=2sinπx（-2≤x≤4）的图象所有交点的横坐标之和等于（　　）

3	x3

与y=x

试题分类